§ 2. Деформация. Кому удобнее на прокрустовом ложе

Согласно мифологической легенде в Аттике жил разбойник Дамаст, по прозвищу Прокруст (вытягиватель). У Прокруста было ложе, на которое он заставлял ложиться тех, кто попадал к нему в плен. Если ложе было слишком длинно, Прокруст вытягивал несчастного до тех пор, пока его ноги не касались края ложа. Если же ложе было коротко, то Прокруст обрубал пленнику ноги.

Ужасная легенда, но вдумайтесь: всем ли так уж страшно прокрустово ложе? Если человек вдвое короче кровати, то ему, конечно, будет не сладко. Если же его рост лишь немного меньше длины ложа, то он вполне может выдержать небольшое дополнительное удлинение. Этот пример ясно показывает, что величину деформации надо оценивать относительной мерой. Забудем на время о Прокрусте и определим точную меру деформации.

Рис. 7

Деформацию характеризуют относительным изменением длины тела ε = Δl/l₀, где l₀ - исходная длина, а Δl - абсолютное изменение длины, разность между конечной длиной и исходной. Величина ε безразмерная и ее удобно выражать в процентах. При одинаковом относительном удлинении тела разной длины испытывают равные деформации ε, а указать лишь приращение длины Δl для характеристики деформированного состояния так же недостаточно, как указать лишь величину нагрузки для характеристики напряженности детали. Даже далекому от техники человеку ясно, что растянуть гвоздь исходной длины 6 мм до 3 м невозможно - он порвется (только в следующей главе мы узнаем, что иногда невозможное возможно!). А вот, например, стальные канаты подвесного моста через залив Форт в Шотландии растянуты именно на 3 м. При их исходной длине около 3 км относительное удлинение составляет всего 0,1%, что вполне допустимо даже для столь ответственной конструкции.

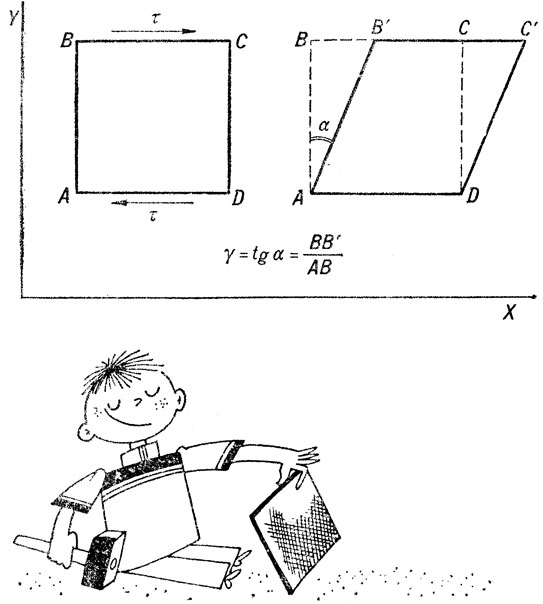
Рис. 8

И, наконец, есть важная подробность и в характеристике деформированного состояния. Чтобы полностью описать деформированное состояние, кроме относительных удлинений, надо узнать и относительные сдвиги, которые могут быть вызваны касательными напряжениями. Например, если мы деформируем кубик так, как показано на рис. 8 (здесь показано изменение формы его передней грани); то первоначально прямой угол BAD становится острым, величина относительного сдвига γ при этом оценивается тангенсом угла ВАВ' (при небольших деформациях - величиной самого угла. Значит, если при определении относительного удлинения мы относили изменение размера вдоль какой-либо оси к исходному размеру вдоль той же оси, то относительный сдвиг γ = tgα находят как изменение размера вдоль оси X, деленное на размер вдоль перпендикулярной ей оси Y. Рис. 8 показывает, кроме того, что сдвиговая деформация вызывает не только изменения углов, но также удлинение (вдоль АС) и укорочение или сжатие (вдоль B'D).