Глава 1. Напряжение и деформация

§ 1. Напряжение. Где тонко, там и рвется

Это утверждение ни у кого не вызывает сомнений. Каждый знает, что тонкую проволочку можно разорвать руками, а толстый канат из этих же проволочек выдержит огромную тяжесть. Так что интуитивно мы хорошо представляем себе, что такое механическое напряжение. И сам этот термин часто используем в разговорной речи: "он без напряжения поднимает двухпудовую гирю", "он покраснел от напряжения".

Рис. 5

Теперь определим это понятие более точно. Напряжением σ называют величину приложенной силы (нагрузку) F, отнесенную к площади поперечного сечения нагруженного тела S:

Таким образом, напряжение имеет размерность (сила/площадь ), в системе СИ - это паскали (1 Па = 1 Н/м²); для нас удобнее будет пользоваться мегапаскалями (1 МПа = 10⁶ Па).

Сама по себе величина нагрузки еще ничего не говорит о результате ее действия. Надо знать, какое напряжение в материале вызовет эта нагрузка. Один и тот же рюкзак кажется легким силачу, у которого большая площадь сечения костей и мышц, и вызывает гораздо большее напряжение в теле обычного человека. В технике чаще всего заранее известна нагрузка, которую будет нести деталь из данного материала, и напряжение, которое для него может быть опасным. Задача конструктора - так выбрать размеры и форму детали, чтобы уровень напряжения не превысил допустимого.

Это все просто и ясно, но есть одна подробность, очень важная для анализа поведения тел при нагружении. Ведь любое тело имеет множество сечений, у каждого из них - своя площадь и, значит, в каждом - свое напряжение. Действительно, если мы будем, например, растягивать цилиндрический стержень двумя одинаковыми силами F, направленными вдоль его оси (рис. 6), то в каждом поперечном сечении площадью S возникнет растягивающее напряжение σ = F/S. Если же мы выберем сечение, перпендикуляр к которому составляет угол α с осью цилиндра, то оно, во-первых, будет иметь уже не круглую форму, а форму эллипса площадью S/cos α, а, во-вторых, сила F будет направлена не перпендикулярно этому сечению, а наклонно.

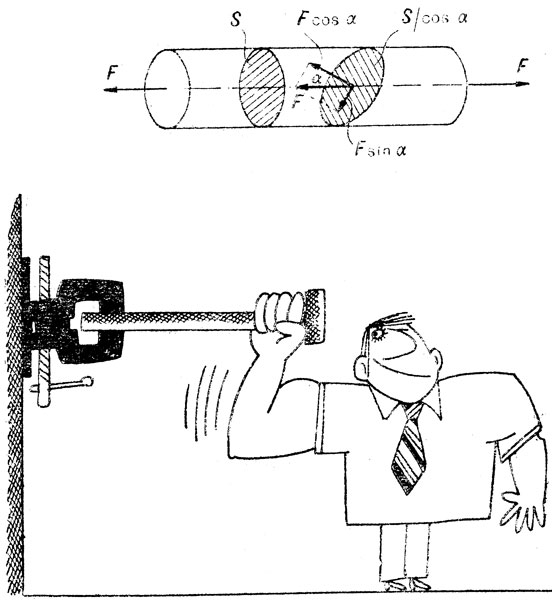
Рис. 6

Пользуясь правилом параллелограмма, легко найдем, что в таких сечениях возникают два напряжения: первое

которое называют нормальным, стремится оторвать эту площадку от соседней, ей параллельной, и второе - его называют касательным или сдвиговым и обозначают

которое стремится сдвинуть эти площадки друг относительно друга.

Отсюда вытекает, что в сечениях, перпендикулярных оси действия нагрузки, действуют только нормальные напряжения σ = P/F (cos α = 1), а касательные напряжения достигают максимума на площадках, наклоненных под углом 45° к оси (так как при α = 45° произведение sinα cosα максимально и равно 1/2). Таким образом, при растяжении максимальные касательные напряжения вдвое меньше максимальных нормальных.

Итак, под нагрузкой заданной величины F стержень с большей площадью поперечного сечения S испытывает меньшие напряжения, чем более тонкий стержень. Если стержень имеет переменное сечение, то в самом тонком месте он и разорвется, так как именно здесь будут действовать наибольшие напряжения.