
§ 5. Упругая и пластическая деформация металлов
Под действием механических нагрузок металлы способны изменять свою форму - деформироваться. В случае небольших нагрузок металлы испытывают упругую Деформацию. Главная особенность упругой деформации заключается в том, что она полностью исчезает после удаления силы, которая ее вызвала, т. е. металл полностью восстанавливает свою форму после прекращения действия приложенной силы. Количественно связь между приложенной силой и вызванной ею упругой деформацией описывается законом Гука.
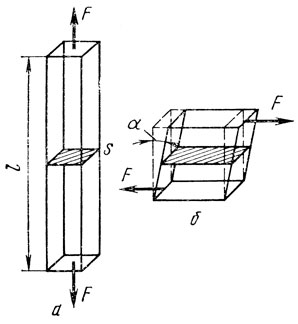
Рис. 6. Схема деформации растяжения (а) и сдвига (б)
Различают два простейших вида упругой деформации- линейное растяжение и простой сдвиг. При линейном растяжении (рис. 6, а) на брусок, имеющий первоначальную длину l и поперечное сечение 5, действует сила F, вызывающая напряжение σ=F/S. Под действием этой силы брусок упруго удлиняется на величину Δl. Закон Гука для этого случая выражается равенством σ = ЕΔl/l = Еε. Здесь ε - относительная упругая деформация, Е - коэффициент пропорциональности. Таким образом, для случая линейного растяжения напряжения растяжения в металле прямо пропорциональны упругому удлинению. При простом сдвиге (рис. 6, б) в образце возникают касательные напряжения τ, которые также пропорциональны деформации, измеряемой тангенсом угла сдвига τ = F/S = Gtg α, где G - также коэффициент пропорциональности. Коэффициент Е называется модулем нормальной упругости Юнга, коэффициент G - модуль сдвига. Оба модуля имеют размерность напряжений (сила/площадь). Они отражают силы связи атомов в решетке и поэтому являются характеристиками, определяемыми природой металла. Значения упругих модулей металлов приведены в табл. 3.
Таблица 3. Упругие свойства металлов
| Металл | Модуль упругости (Юнта), Е, ГПа | Модуль сдвига G, ГПа |
| Алюминий | 70 | 27 |
| Бериллий | 300 | 150 |
| Ванадий | 130 | 47 |
| Вольфрам | 400 | 145 |
| Гафний | 140 | - |
| Железо | 200 | 80 |
| Золото | 80 | 28 |
| Кобальт | 210 | 76 |
| Кремний | 110 | - |
| Магний | 45 | 17 |
| Медь | 125 | 45 |
| Молибден | 350 | 119 |
| Никель | 200 | 80 |
| Ниобий | 100 | 37 |
| Олово | 47 | 15 |
| Платина | 160 | 60 |
| Рений | 460 | - |
| Свинец | 18 | 8 |
| Серебро | 80 | 28 |
| Тантал | 180 | 70 |
| Титан | 110 | 45 |
| Хром | 250 | - |
| Цинк | 90 | 36 |
| Цирконий | 97 | 35 |
Примечание. ГПа = 109 Па.
При полиморфных превращениях значения модулей меняются незначительно. Это объясняется тем, что природа атомов при этом не меняется, а изменение объема и связанное с этим изменение числа атомов, приходящегося на единицу объема в кристаллической решетке, не превышает нескольких процентов. Значения модулей упругости и сдвига, определенные по разным направлениям в монокристалле, существенно различаются. Эти различия связаны с разной плотностью упаковки кристаллических плоскостей. Легирование металла, т. е. введение в него других элементов, сказывается на упругих характеристиках пропорционально доле введенных атомов, поэтому модули упругости и сдвига малолегированных сплавов практически равны модулям чистых металлов, являющихся основами этих сплавов.
Модули упругости и сдвига представляют собой важнейшие характеристики металлов, предопределяющие так называемую жесткость металлических конструкций и деталей. Значение модуля упругости можно видеть из следующего примера. Если одна и та же деталь изготовлена из вольфрама, стали и сплава на основе меди, то одинаковые напряжения вызовут в ней различные упругие деформации, величины которых будут относиться (по закону Гука) обратно пропорционально модулям упругости материалов, т. е. как 1:2:3.
Если на металл действует большие напряжения, то после снятия нагрузки форма и размеры металлического изделия, детали или образца не возвращаются к первоначальным, существовавшим до приложения нагрузки. Это означает, что металл испытал пластическую деформацию. По мере дальнейшего увеличения напряжений возрастает и пластическая деформация, а затем происходит разрушение металла.
Строго говоря, в большинстве случаев самые небольшие напряжения уже способны вызвать в металле некоторую пластическую деформацию, но для упрощения расчетов допускают, что при нарастании действующих напряжений металл вначале деформируется только упруго, а затем - пластически.
Теоретические представления, экспериментальные данные и практические наблюдения показывают, что при любых способах механических воздействий на металл пластическая деформация в нем происходит путем скольжения и двойникования. На рис. 7 представлена схема процесса пластической деформации кубического кристалла путем скольжения. Положение а представляет собой кристаллическую решетку в исходном состоянии. После приложения нагрузки (положение б) под действием сдвигающих (иначе скалывающих) напряжений кристалл деформируется упруго, при этом все ячейки кубической решетки приобретают вид ромбов, а расстояния между горизонтальными плоскостями уменьшаются. По мере возрастания приложенной нагрузки скалывающие напряжения растут, и упругая деформация кристаллической решетки увеличивается, пока, наконец, не произойдет смещение верхней части кристалла относительно нижней на одно межатомное расстояние. Касательное напряжение, вызвавшее это первоначальное смещение, называется критическим напряжением сдвига или критическим скалывающим напряжением. Плоскость, по которой произошло смещение, называется плоскостью скольжения. На рис. 7 она перпендикулярна плоскости чертежа. Ее след обозначен пунктирной линией (положения в и г). Направление скольжения в данном случае совпадает с направлением приложенной к кристаллу силы, которая указана стрелками. Если после происшедшего скольжения снять нагрузку, действовавшую на кристалл, то упругая деформация полностью исчезнет, элементарные ячейки примут первоначальную форму кубов (на рисунке - квадратов), форма же всего кристалла останется измененной; в нем прошла пластическая деформация. Если бы нагрузка продолжала действовать, то скольжение происходило бы и дальше, и верхняя часть сдвигалась относительно нижней на два, три и т. д. межатомных расстояния.
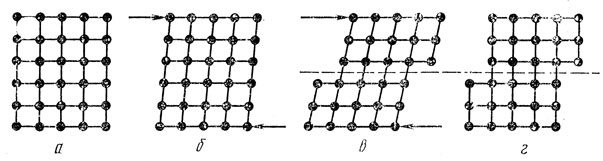
Рис. 7. Пластическая деформация кристалла скольжением
Схема пластической деформации кристалла путем двойникования представлена на рис. 8, где действующие на кристалл силы изображены стрелками. Упругая деформация, предшествовавшая пластической, на рисунке не показана. Пластическая деформация прошла в правой верхней части кристалла, она выразилась в закономерном смещении атомов в диагональных плоскостях элементарных ячеек. Первоначальное положение атомов в этой части кристалла изображено знаком плюс. Плоскость, отделяющая незатронутую деформацией часть кристалла от части, подвергшейся деформации, называют плоскостью двойникования. Она перпендикулярна плоскости рисунка, ее след отмечен пунктирной линией.
Нетрудно убедиться в том, что в результате прошедшей пластической деформации правая верхняя часть кристалла стала как бы зеркальным отражением левой части, т. е. из одного кристалла образовалось два, причем их взаимное расположение строго определено. В кристаллографии такие кристаллы называют двойниками, отсюда появился термин двойникование. Пластическая деформация путем двойникования по существу происходит за счет скольжения, которое охватывает сразу множество плоскостей, смещающихся одна относительно другой в определенной закономерности. Эта закономерность на рис. 8 заключается в том, что каждая атомная плоскость, параллельная плоскости двойникования, смещается относительно соседней плоскости на 1/2 межатомного расстояния в направлении двойникования. На рис. 8 направление двойникования совпадает с направлением действующих сил.
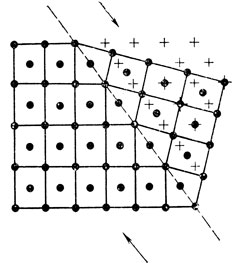
Рис. 8. Пластическая деформация кристалла двойникованием
Плоскости и направления скольжения и двойникования в значительной мере предопределяются типом кристаллической решетки. При механическом воздействии на кристалл скольжение будет происходить при наименьших нагрузках по тем плоскостям, которые отстоят одна от другой на наибольшие расстояния. Из изложенного в § 2 следует, что такие плоскости в кристаллических решетках являются наиболее плотноупакованными. Следовательно, скольжение должно происходить по плоскостям с плотнейшей упаковкой. Направление скольжения всегда совпадает с тем направлением в решетке, которое наиболее плотно усеяно атомами.
Таким образом, в металлах с гранецентрированной кубической решеткой плоскостями скольжения являются октаэдрические плоскости {111}, а направлением скольжения - диагонали грани куба <110>. В металлах с объемноцентрированной кубической решеткой скольжение может происходить по нескольким семействам плоскостей - {110}, {112}, {113}, но всегда в направлении <111>. Скольжение в металлах с гексагональной плотноупакованной решеткой происходит по плоскости базиса {0001} в каком-либо одном из трех направлений <1010>.
Двойникование в г. ц. к. решетке происходит по плоскостям {111}в направлении <112>, в о. ц. к. решетке - по {112} и <111>, в г. п. у. решетке по {1012} и <0111>.
Из схемы скольжения, изображенной на рис. 7, следует, что при перемещении верхней части кристалла на одно межатомное расстояние каждый раз происходит разрыв и немедленное последующее восстановление связей между всеми атомами, разделяемыми плоскостью скольжения. Теоретические расчеты показали, что для этого необходимы нагрузки, дающие высокие критические напряжения сдвига, которые превосходят экспериментальные данные в 100 - 1000 раз. Согласовать опытные и теоретические данные удается, если использовать представления о дислокациях.
На рис. 9, а изображен кристалл, подобный тому, который был на рис. 7. Под действием нагрузки в кристалле появилась краевая дислокация, проходящая перпендикулярно чертежу. В данном случае, чтобы вызвать скольжение верхней части кристалла относительно нижней, не нужно разрывать сразу все межатомные связи на плоскости скольжения. Уже при очень небольшой нагрузке будет происходить перемещение (скольжение) краевой дислокации слева направо (рис. 9, б и в), так как атомы в районе дислокации уже смещены из положений равновесия. В результате дислокация пробегает весь кристалл и выходит на поверхность, создавая там ступеньку в одно межатомное расстояние (рис. 9, г). Как видно, в итоге получается то же положение, что и на рис. 7, т. е. в результате Перемещения дислокации изменилась форма кристалла, в нем прошла пластическая деформация.
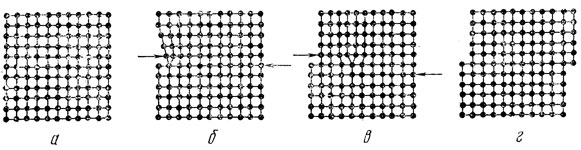
Рис. 9. Пластическая деформация кристалла с краевой дислокацией
В наиболее совершенных металлических кристаллах может быть 103 - 105 дислокаций на 1 см2. В результате пластической деформации плотность дислокаций возрастает до 109 - 1011 на 1 см2. Дело в том, что на рис. 7 - 9 изображены идеализированные схемы, когда на кристалл действуют нагрузки, вызывающие только касательные напряжения. Фактически даже деформация монокристалла простым растяжением вызывает появление в нем большого количества новых дислокаций. Увеличение плотности дислокаций обусловливает все более сильное упругое взаимодействие между ними. В результате по мере роста пластической деформации требуются все большие нагрузки для ее продолжения. Такое упрочнение металлического кристалла называют наклепом. Наконец, в кристалле исчерпывается способность к пластической деформации как путем скольжения, так и путем двойникования, и если нагрузка будет увеличиваться, кристалл разрушится.
Из обсуждения пластической деформации металлических монокристаллов ясно, что в поликристаллических образцах она должна проходить очень сложно. Прежде всего следует отметить большую неоднородность прохождения пластической деформации в начальной стадии.
При линейном растяжении поликристаллического образца (см. рис. 6) после определенной упругой деформации, которая захватит все зерна, в некоторых из них начнется пластическая деформация. Из курса сопротивления материалов известно, что при линейном растяжении в образце развиваются тангенциальные (касательные) напряжения. Они достигают наибольшей величины в направлениях под 45° к оси растяжения. По этой причине те зерна в образце, у которых направления и плоскости легкого скольжения расположены под углом в 45° к оси растяжения, начнут деформироваться пластически, в то время как в других кристаллах, расположенных иным образом, будет продолжаться упругая деформация. Пластически деформируемые зерна будут упрочняться - наклёпываться, и, кроме того, в ходе деформирования всего образца их ориентировка будет меняться. По этим причинам после растяжения образца на некоторую величину действующие напряжения оказываются не в состоянии вызывать в них пластическую деформацию, и они вновь начнут деформироваться упруго. Но к этому моменту другие зерна, которые пока деформировались только упруго, в ходе растяжения образца изменили свое расположение. У некоторых из них направления и плоскости легкого скольжения оказались под углом в 45° к оси растяжения, и эти зерна начали деформироваться пластически. По мере общего удлинения образца в ходе растяжения пластическая деформация захватывает все новые и новые зерна. Если напряжения растяжения будут увеличиваться, то пластическая деформация может происходить во всех зернах, в том числе и в тех, которые ориентированы самым неблагоприятным для данных условий образом. При деформации поликристаллических образцов скольжение и двойникование могут происходить не только по плоскостям и направлениям наиболее легкого деформирования, но и по некоторым другим системам. Такая усложненность пластической деформации вызывает быстрое упрочнение металла.
Опыт показывает, что скольжение не проходит равномерно, а захватывает отдельные области в поликристаллическом металле, Эти участки можно различать простым глазом или под небольшим увеличением, например, на поверхности образцов, подвергнутых растяжению. Они носят название полос Чернова-Людерса и расположены под углом 45° к оси растяжения, так как именно под этим углом в образце развиваются наибольшие касательные напряжения.
Под действием пластической деформации в кристаллической решетке происходят серьезные изменения: плоскости сильно изгибаются, между отдельными участками решетки возникают большие упругие напряжения, весь объем кристалла разбивается на очень мелкие участки (не более 1 - 3 мкм), на границах которых скапливаются дислокации и другие несовершенства, внутри же этих микрообъемов кристаллическая структура сохраняется достаточно совершенной.
Все сказанное относится к так называемой холодной деформации, проходящей при низких температурах. Для металлов технической чистоты условная граница между низкими и высокими температурами лежит около 0,4 Тпл. При повышении чистоты эта температура заметно понижается. Для сплавов она доходит до 0,6 Тпл. Влияние повышения температуры на пластическую деформацию выражается прежде всего в том, что снижаются критические скалывающие напряжения. Сдвиги и двойникование совершаются при меньших внешних нагрузках. Кроме того, начинают работать дополнительные системы скольжения, и это также облегчает пластическую деформацию металла. Наконец, если температура, при которой осуществляется деформация, достаточно высока, то в результате возросшей диффузионной подвижности атомов все или почти все дефекты, вызываемые пластической деформацией, в виде дислокаций, искажений атомных плоскостей, напряжений между блоками и между зернами, успевают уничтожиться. Это означает, что в ходе такой горячей деформации металл не упрочняется. Таким образом, пластическая деформация при высоких температурах характеризуется существенно меньшими напряжениями сдвига и отсутствием наклепа.
Время действия нагрузки может существенно повлиять на процесс пластической деформации металлов. Если нагрузка действует в течение сотен и тысяч часов, то пластическая деформация может обнаружиться при очень малых напряжениях. Особенно велика роль времени при температурах, близких к 0,4 Тпл и выше. Б этих условиях из-за повышенной диффузионной подвижности атомов при очень небольших напряжениях (в 10 - 100 раз меньших, чем при комнатной температуре) в кристаллической решетке начинается передвижение дислокаций и просто направленное перемещение атомов, в результате чего происходит пластическая деформация. В этих условиях не происходит накопление дефектов в кристаллической решетке, и металл не упрочняется.
|
ПОИСК:
|
© METALLURGU.RU, 2010-2020
При использовании материалов сайта активная ссылка обязательна:
http://metallurgu.ru/ 'Библиотека по металлургии'
При использовании материалов сайта активная ссылка обязательна:
http://metallurgu.ru/ 'Библиотека по металлургии'