§ 2. Кристаллическая структура металлов

Как указывалось, при сближении достаточно большого числа атомов металла они располагаются в пространстве в определенном порядке. Объем вещества, в котором атомы расположены упорядоченно по одной схеме, называется кристаллом. Все металлы являются кристаллическими веществами. Упорядоченное расположение атомов (правильнее, ионов) металла называется его кристаллической структурой. Поскольку взаимодействие между ионами металлов и свободными электронами зависит от заряда и массы ядер атомов, количества свободных электронов и их энергий, то понятно, что вид кристаллической структуры у разных металлов в общем случае различен. Вместе с тем можно ожидать, что из-за сходства в строении внешних электронных оболочек, из которых образуются свободные электроны, разные металлы могут иметь одинаковую кристаллическую структуру. Изменение температуры может вызвать смену кристаллической структуры из-за того, что именно температура предопределяет интенсивность колебаний ионов, а от этого в основном зависят способ взаимного расположения ионов и расстояние между ними.

Кристаллическая структура может быть изображена в виде кристаллической решетки, которая представляет собой воображаемую трехмерную сетку, образованную рядами атомов (ионов). Если мысленно соединить центры атомов прямыми линиями и провести плоскости, объединяющие эти линии, то вся кристаллическая решетка будет разбита на многогранники, в вершинах которых находятся атомы. Точка, в которой находится атом, называется узлом решетки. Такие многогранники наименьших для данной решетки размеров называются примитивной ячейкой решетки. Практически для описания решеток пользуются элементарной кристаллической ячейкой, которая более сложна, чем примитивная, включает в себя большее число атомов и более полно отражает симметрию решетки, т. е. число и порядок осей симметрии. Осью симметрии называют воображаемую ось, при повороте вокруг которой наблюдается полное совпадение элементов геометрической фигуры - точек ребер, граней. Порядок данной оси симметрии определяется числом таких совпадений при повороте фигуры на 360°. В кристаллических решетках обнаруживаются оси симметрии 2-го, 3-го, 4-го, 6-го порядков.

Элементарная ячейка полностью характеризует кристаллическую решетку. Путем последовательного присоединения элементарных ячеек данная кристаллическая решетка может быть распространена на любой объем. Тип и название элементарной ячейки переносятся на тип и название кристаллической решетки.

Для металлов характерны следующие кристаллические решетки: гранецентрированная кубическая (г. ц. к.), объемноцентрированная кубическая (о. ц. к.), гексагональная плотноупакованная (г. п. у). На рис. 2 представлены элементарные ячейки этих решеток, а также элементарные ячейки тетрагональной объемноцентрированной и ромбоэдрической решеток. Эти решетки также встречаются у металлов. Здесь же представлена элементарная ячейка кубической решетки алмаза. Эта кристаллическая решетка характерна для структуры многих полупроводников.

Элементарная ячейка гранецентрированной кубической решетки (рис. 2, а) представляет собой куб с ребром а. В вершинах куба находятся 8 атомов. Кроме того, в центре каждой из 6 граней находится по одному атому. Ребро а называется периодом решетки. Гранецентрированную кубическую решетку имеют, медь, никель, алюминий, свинец, железо в интервале 910 - 1390°С (γ-железо), серебро, золото, палладий, платина и др.

Элементарная ячейка объемноцентрированной кубической (о. ц. к) решетки (рис. 2, б) представляет собой куб с 8 атомами в вершинах и 1 атомом в центре на пересечении объемных диагоналей. Периодом решетки считается ребро куба а. такой, решеткой обладают железо (α-железо до 910°С и δ-железо от 1390°С до точки плавления), хром, молибден, вольфрам, ванадий, ниобий, тантал, высокотемпературные β-модификации титана, циркония, гафния от температур соответственно 882, 865, 1700°С до точек плавления, литий, калий, натрий и др.

Элементарная ячейка гексагональной плотноупакованной решетки (рис. 2, в) представляет собой правильную шестигранную призму с 12 атомами в вершинах. Шестиугольные основания, называемые базисом, можно представить состоящими из шести равносторонних треугольников с общей вершиной в центре шестиугольника. В этой точке находятся еще по одному атому в верхнем и нижнем основании. Кроме того, внутри ячейки находятся еще три атома, расположенные в плоскости, проходящей по середине высоты призмы. Если из точек, занимаемых этими тремя атомами, опустить перпендикуляры на основания, то они попадут в центры трех из шести треугольников. Атомы в указанной средней плоскости расположены относительно друг друга точно так же, как и атомы в основаниях призмы. В этом нетрудно убедиться, если пристроить к данной ячейке еще несколько элементарных призм.

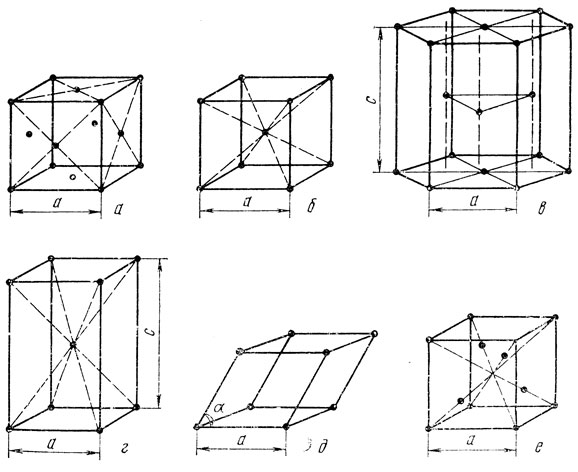
Рис. 2. Элементарные ячейки кристаллических решеток

Элементарная ячейка гексагональной плотноупакованной решетки характеризуется двумя размерами: а и с. Период а - сторона шестиугольного основания призмы, с - высота призмы. Если считать, что атомы представляют собой жесткие шары и уложены вплотную по описанной схеме, то отношение с/а = 1,633. Строго говоря, только при этом условии можно называть гексагональную решетку плотноупакованной. В решетках реальных металлов это отношение, как правило, либо меньше, либо больше этой величины, тем не менее обычно их называют плотноупакованными. Гексагональную плотноупакованную решетку имеют магний, цинк, кадмий, бериллий, низкотемпературные α-модификации титана, циркония, гафния, рений и др. Гексагональная плотноупакованная решетка представляет один из двух способов наиплотнейшей укладки атомов, если считать их жесткими шарами. Другой способ наиплотнейшей укладки осуществляется в уже описанной кубической гранецентрированной решетке. Во всех других решетках некоторые атомы шары расположены невплотную один к другому, и поэтому все остальные решетки называют рыхлыми в отличие от этих двух.

Элементарная ячейка тетрагональной объемноцентрированной решетки (рис. 2, г) представляет собой прямоугольную призму с квадратным основанием. Кроме восьми атомов в вершинах, в этой ячейке имеется еще один атом, расположенный в центре призмы, на пересечении объемных диагоналей. Ячейку определяют периоды а и с - сторона квадрата в основании и высота призмы соответственно. Тетрагональную объемноцентрированную решетку имеют олово ("белое" β-олово, устойчивое выше 13°С), индий.

Элементарная ячейка ромбоэдрической решетки (рис. 2, д) представляет собой шестигранник, у которого все грани являются одинаковыми ромбами. Ромбоэдрическую ячейку легко представить как простой куб, деформированный вдоль одной из своих диагоналей. Эта ячейка характеризуется величиной ребра ромбоэдра - периодом а и острым углом при вершине. Ромбоэдрической решеткой обладают ртуть, мышьяк, сурьма, висмут.

Элементарная ячейка кубической алмазной решетки (рис. 2, е) является гранецентрированным кубом с четырьмя атомами внутри. Эти четыре атома расположены попарно в двух вертикальных плоскостях на диагоналях куба на расстояниях в ¹/₄ диагонали от верхней и нижней граней. В этой ячейке каждый атом имеет по четыре ближайших соседа, находящихся на расстоянии а√3/4, где а - ребро куба, являющееся периодом решетки. Подобную решетку имеют алмаз, германий, кремний, "серое" α-олово, устойчивое ниже 13°С.

Периоды кристаллических решеток измеряют в нм (нанометрах).

Для сопоставления физических свойств металлов большое значение имеет число атомов, приходящееся на одну элементарную ячейку, и доля объема в ячейке, занятого собственно атомами. Рассматривая элементарную ячейку г. ц. к. решетки (см. рис. 2) можно видеть, что на одну ячейку приходится 4 атома: каждый из 8 атомов на вершинах принадлежит 8 ячейкам, поэтому на данную ячейку приходится 8/8 = 1 атом, каждый из 6 атомов на гранях принадлежит двум ячейкам, поэтому на данную ячейку приходится 6/2 = 3; итого 1+3 = 4. В о. ц. к. решетке на одну элементарную ячейку приходятся только два атома: как и в г. ц. к. решетке один атом получается от восьми атомов в вершинах куба и один атом в центре куба.

В г. п. у. решетке на одну элементарную ячейку приходится 6 атомов: 3 (внутри) +2/2 (в центре оснований) + 12/6 (в вершинах) = 6.

Доля объема в ячейке, занятого собственно атомами, называется коэффициентом заполнения решетки. Этот коэффициент определяется из условия, что атомы являются жесткими шарами и уложены вплотную по той схеме, которая характерна для данной решетки. Путем несложных геометрических построении и расчетов можно показать, что коэффициент заполнения в г. ц. к. решетке составляет 74%, в о. ц. к. решетке - 68%, в г. п. у. решетке при с/а = 1,633 - 74%, в кубической алмазной решетке - всего 34%.

Кристаллические решетки можно характеризовать также координационным числом, которое показывает число ближайших соседей у каждого атома, находящихся на одинаковых от него расстояниях. В случае гранецентрированной кубической решетки наименьшее расстояние между атомами равно а√2/2 - половине диагонали грани куба. Для любого атома, например занимающего положение в центре горизонтальной грани, имеются 4 подобных ближайших соседа в горизонтальной плоскости (см. рис. 2, а), 4 таких же соседа в вертикальной плоскости, совпадающей с плоскостью рисунка (два атома имеются на рисунке, другие два выявляются, если пристроить еще одну ячейку снизу), еще четыре соседа находятся в вертикальной плоскости, перпендикулярной плоскости чертежа (опять два из них видны на чертеже, другие два выявляются при пристройке еще одной ячейки снизу). Таким образом, всего ближайших соседей оказывается 12, и координационное число гранецентрированной кубической решетки равно 12.

В приведенном примере в качестве центрального атома, для которого определялось число ближайших соседей, был выбран один из атомов в центре грани. Можно было бы взять любой атом в вершине куба, результат получился бы такой же. Это происходит потому, что все атомы в данной решетке совершенно равноценны.

В случае объемноцентрированной кубической решетки очень легко и наглядно можно определить кратчайшее расстояние и число ближайших соседей, если взять за точку отсчета центральный атом, находящийся на пересечении объемных диагоналей куба. На рис. 2, б ясно видно, что кратчайшее расстояние равно половине диагонали куба а√3/2, число ближайших соседей - 8 и координационное число равно 8. Еще раз можно отметить, что ввиду равноценности атомов можно было вести отсчет от атома в вершине куба и получить тот же результат.

Несколько сложнее определить числа ближайших соседей в гексагональной плотноупакованной решетке. За точку отсчета разумно взять атом, находящийся в центре нижнего основания призмы - элементарной ячейки. Очевидно, у этого атома в горизонтальной плоскости в углах шестиугольного основания на расстоянии а имеются шесть ближайших соседей (рис.2, б). Кроме того, имеются еще шесть ближайших соседей - три атома внутри призмы (на рисунке) и еще три таких же атома в ячейке, которая должна примыкать снизу к изображенной на рисунке. Можно показать, что эти шесть атомов находятся также на расстоянии а от атома, вы бранного за точку отсчета. Таким образом, оказывается, что координационное число в данном случае равно 12.

Следует отметить, что совпадение коэффициента заполнения и координационного числа у гранецентрированной кубической и плотноупакованной гексагональной решеток не случайно. Как уже отмечалось, именно в этих двух решетках расположение атомов соответствует наиплотнейшей укладке шаров одного размера.

Из приведенного описания видно, что некоторые металлы могут иметь разные решетки в зависимости от температуры. Так, титан, цирконий, гафний при низких температурах обладают гексагональной плотноупакованной решеткой, а при высоких - объемноцентрированной кубической. В железе наблюдается двукратное изменение решетки: при 910°С о. ц. к. решетка сменяется на г. ц. к., а при 1390°С атомы вновь выстраиваются по схеме о. ц. к. решетки. Подобные превращения называют аллотропическими или полиморфными. Металл также называют полиморфным, обладающим различными кристаллическими модификациями. Эти модификации обозначаются первыми буквами греческого алфавита - α, β, γ, δ, причем α-модификацией всегда называется низкотемпературная форма.

Из приведенного описания видно, что атомы в кристаллических решетках расположены рядами, которые могут быть объединены в отдельные плоскости. Для того чтобы описывать эти ряды и плоскости, пользуются специальными правилами. Для кубических решеток применяется система индексов Миллера, основанная на использовании прямоугольной трехосной системы координат.

Поместим начало координат в вершину элементарной кубической ячейки (в точку 1 на рис. 3, а), а оси X, Y, Z направим на ребра куба. Положение любой плоскости описывают с помощью трех индексов, которые представляют величины, обратные длинам отрезков, отсекаемых данной плоскостью на осях координат. При этом отрезки измеряются в периодах решетки по данной оси, а индексы приводятся к простым целым числам. Найдем индексы плоскости, образующей грань куба, проходящую через атомы 2-3-7-6. Эта плоскость параллельна оси X, поэтому формально записывают, что она отсекает на ней бесконечно большой отрезок . По оси Y эта плоскость отсекает отрезок длиной 1, а по оси Z - . Таким образом длины отсекаемых отрезков по трем осям будут , 1, , а величины обратные им 0, 1, 0. Индексы рассматриваемой плоскости записывают в круглых скобках подряд (010) и читают "ноль - один-ноль". Плоскость, проходящая по точкам 3-4-8-7, отсекает на осях X, У, Z отрезки 1, . Следовательно, ее индексы будут (100). Плоскость 5-6-7-8 отсекает отрезки на осях координат 1. Ее индексы (001).

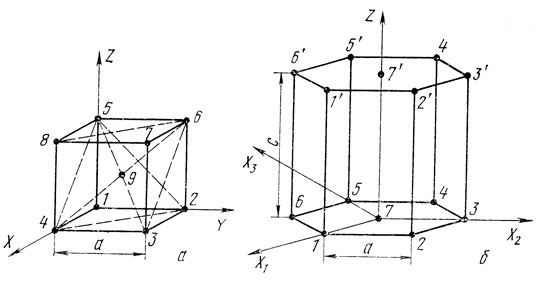
Рис. 3. Схема к выводу обозначений плоскостей и направлений в кристаллических решетках

Принятая система обозначения плоскостей с помощью индексов Миллера позволяет переносить начало системы координат без поворота осей в любую точку кристаллической решетки, и эта операция не изменяет индекса плоскостей. Например, если перенести начало координат на рис. 3, а из точки 1 в точку 9, то плоскость, образующая грань куба 2-3-7-6, будет параллельна осям X и Z, а на оси Y отсечет отрезок, равный 1/2. Следовательно, отсекаемые на осях отрезки будут , 1/2, . Обратные им величины получаются такими: 0, 2, 0. После приведения к простым целым числам (делением всех трех индексов на 2) имеем окончательно индексы плоскости 2-3-7-6 (010). Как видно, они совершенно одинаковы с индексами этой плоскости в предыдущем случае, когда начало координат находилось в точке 1.

Если рассматриваемая плоскость отсекает отрезок на отрицательном направлении данной оси координат, то в значениях индексов появляются величины со знаком минус. Пусть начало координат находится в точке 9. Плоскость 1-4-8-5 параллельна осям X и Z. На оси У она отсекает отрезок, равный минус 1/2. Следовательно, отрезки, отсекаемые по трем осям, будут , -1/2, , а индексы (010). Знак минус в обозначениях индексов пишется над цифрой и читается перед ней, в данном случае - "ноль - минус один - ноль". Пользуясь описанными правилами, можно обозначить индексы всех шести плоскостей куба:

Плоскость	Отсекаемые на осях X,Y,Z отрезки (начало координат в точке 9)	Индексы плоскости
2-3-7-6	, -1/2,	(010)
1-4-8-5	, -1/2,	(010)
3-4-8-7	1/2, ,	(100)
1-5-6-2	-1/2, ,	(100)
5-6-7-8	, , 1/2	(001)
1-2-3-4	, , -1/2	(001)

На рис. 3 видно, что все грани куба совершенно одинаковы по способу размещения атомов, по числу атомов и по взаимному расположению. Формально это отражается в их индексах, которые во всех случаях состоят из двух нулей и одной единицы (с плюсом или минусом). Вся совокупность подобных одноименных плоскостей называется семейством плоскостей и обозначается индексами в фигурных скобках {001}.

Выявим еще два важных семейства плоскостей в кубической решетке. Рассмотрим плоскость 2-4-8-6 на рис. 3, а. Она включает в себя и центральный атом 9. Если начало координат находится в точке 1, то отрезки, отсекаемые этой плоскостью на осях X, Y, Z, равны 1, 1, . Следовательно, индексы этой плоскости (ПО). Таких плоскостей в кубической решетке с учетом отрицательных индексов насчитывается 12. Эта плоскость называется плоскостью ромбического додекаэдра, так как с ее помощью можно построить правильный 12-гранник с гранями в виде ромба. Семейство плоскостей ромбического додекаэдра обозначается {110}.

Рассмотрим плоскость, проходящую через точки 2-4-5 (следует иметь в виду, что в эту плоскость не попадает центральный атом 9). Она отсекает на всех осях координат одинаковые отрезки а, следовательно, ее индексы будут (111). Таких плоскостей в кубической решетке восемь, они называются плоскостями октаэдра, так как с их помощью можно построить правильный восьмигранник. Грань октаэдра представляет собой разносторонний треугольник.

Рассмотрим обозначение плоскостей в гексагональной решетке (рис. 3, б). В этом случае более удобна иная система (Миллера-Браве) с четырьмя осями координат, три из которых лежат в одной плоскости под углом 120° одна к другой, а четвертая ось перпендикулярна им. Начало координат помещается в точку, занимаемую центральным атомом в основании шестигранной призмы - элементарной ячейки данной решетки. Три оси, обозначаемые Х₁, Х₂, Х₃, проходят через вершины ячейки, ось Z направлена перпендикулярно основанию - базису. Индексы плоскостей и в этом случае определяются как величины, обратные отрезкам, отсекаемым на осях координат, но так как здесь имеются четыре оси, то индексы будут четырехзначными. Плоскость грани 1-2-1'-2' отсекает на оси Х₁ отрезок 1а, на оси Х₂ - , на оси Х₃ - минус 1а, на оси Z - . Поэтому ее индексы будут (1010). Плоскости всех шести граней призмы объединяются в одно семейство {1100}. Плоскости базиса ячейки будут обозначаться {0001}, так как они параллельны трем осям Х₁, Х₂, Х₃ и отсекают отрезки только на оси Z.

Для характеристики кристаллической решетки необходимо уметь обозначать направления, в которых располагаются ряды атомов или отдельные атомы относительно выбранного начала координат. Для этого из начала координат до рассматриваемой точки проводят вектор и затем проектируют его на оси координат. Получаемые значения проекции выражают в периодах решетки на данной оси и записывают в виде наименьших целых чисел в квадратных скобках, чтобы отличить от индексов плоскостей. Определим направление, в котором лежит атом 7 в кубической решетке, элементарная ячейка которой изображена на рис. 3, а. Проекции точки 7 на оси координат будут 1, 1, 1, следовательно, индексы направления будут [111]. Центральный атом 9 имеет такое же направление, так как его проекции будут 1/2, 1/2, 1/2, следовательно, индексы будут также [111]. Из рисунка видно, что оба атома 7 и 9 действительно лежат на одной прямой, являющейся диагональю куба, и индекс [111] указывает направление этого ряда атомов. На правления могут проектироваться на отрицательные части осей, в этом случае появляются отрицательные индексы. В кубических решетках насчитывается восемь направлений рассматриваемого типа. Все они объединяются в семейство, индекс которого указывается в угловых скобках <111>. Направление диагонали грани куба, проходящей от точки 1 к точке 8, запишется как [101], поскольку проекции точки 8 на оси координат будут 1, 0, 1. Таких направлений в кубической решетке 12, их семейство обозначается <011>. Направление ребра куба 1 - 2 обозначается [010]. Семейство <001> насчитывает шесть конкретных направлений.

Важной особенностью принятой системы обозначения направлений является то, что численно индекс направления совпадает с индексом плоскости, к которой данное направление перпендикулярно. Так, направление [111] и плоскость (111) взаимно перпендикулярны, также как и направление [110] и плоскость (110), направление [100] и плоскость (100).

Для обозначения направлений в гексагональных решетках используется аналогичный принцип, и если применяются четырехзначные индексы Миллера-Браве, то обозначения взаимно перпендикулярных плоскостей и направлений совпадают.

В кристаллической решетке вообще можно провести и исследовать сколь угодно много плоскостей и направлений, индексы которых могут выражаться сочетанием любых целых чисел. Однако опыт показывает, что наибольшую роль в определении физических и механических свойств металлических кристаллов играют плоскости и направления, в которых на единицу длины или площади приходится наибольшее число атомов, т. е. обладающие наиболее плотной упаковкой.

В гранецентрированной кубической решетке наиболее плотноупакованными плоскостями являются плоскости октаэдра {111}, а наиболее плотноупакованными направлениями <110>. В объемноцентрированной кубической решетке наиболее плотно упакованы плоскости -{110}- и направления <111>. В гексагональной плотноупакованной решетке с отношением с/а = 1,633 и координационным числом 12 плотнейшей плоскостью является базис {0001}, а плотнейшими направлениями <1120>. Эти направления совпадают с осями координат Х₁, Х₂, Х₃ на рис. 3, б.

Гидрораспределитель золотниковый ВЕХ16.14 линк.