§ 4. Трещина Гриффитса

В те годы А. Гриффите (1893 - 1963) работал инженером в одном из авиационных исследовательских центров и занимался исследованиями прочности стекла. Стекло не использовалось в авиастроении в качестве конструкционного материала и служило Гриффитсу моделью, на которой можно было получить идеально хрупкое разрушение. Руководители центра не одобряли "увлечения" Гриффитса и, когда горелка, на которой он плавил стекло, стала причиной пожара в лаборатории, его опыты были запрещены, а сам он переведен на другую работу. Но все же Гриффите успел получить результаты, на которых базируется вся современная физическая теория хрупкого разрушения.

Анализ Гриффитса был удивительно простым и ясным. Убедившись в том, что без трещин ему не обойтись, он составил уравнение баланса энергии в нагруженной пластине, в которой возникает и растет трещина. Чтобы повторить его расчет, мы можем воспользоваться рис. 83. Итак, если пластина находится под действием напряжения σ, не превышающего предела упругости, то соответствующую упругую деформацию мы можем определить из закона Гука:

Упругая энергия, которая запасена в единице объема пластины, как мы знаем, равна

Когда в пластине возникает трещина длиной 2с (рис. 83), то некоторый объем материала "разгружается" (помните, отлынивает от работы), а другие оказываются перегруженными. Но баланс упругой энергии в целом изменяется в сторону ее уменьшения^*). Таким образом, мы можем считать, что полное изменение упругой энергии пластины вызвано разгрузкой некоторого (эффективного) объема материала, размеры которого сопоставимы с длиной трещины. Гриффите принял, что этот объем ограничен эллипсом с полуосями с и 2с. Площадь этого эллипса равна 2πс², а интересующий нас объем 2πс²В, где В - толщина пластины. Значит, образование трещины вызвало выделение упругой энергии

^*(Это легко пенять, если мы учтем, что когда трещина разорвет пластину пополам, обе половины вообще будут разгружены, их упругая деформация исчезнет.)

Немного фантазии - и мы можем считать, что вся эта энергия "поселилась внутри" трещины. Вот мы и установили, что за "змей" живет в трещине.

Куда расходуется эта энергия? Гриффите резонно предположил, что она идет на образование двух новых поверхностей - "берегов" трещины. Ведь поверхность всегда обладает повышенной энергией; это знает каждый, кто имел дело с мыльными пузырями. Для того чтобы раздуть пузырь, надо совершить работу против сил поверхностного натяжения. Следовательно, поверхность обладает избыточной энергией, только у металлов поверхностная энергия, которая приходится на единицу площади, в 10 - 20 раз больше, чем у мыльной пленки. Эту удельную поверхностную энергию обозначим γ_s. Поскольку при возникновении трещины образовались две новые поверхности, каждая площадью 2 сВ (кривизной берегов трещины пренебрегаем), нужно затратить энергию 4 cBγ_s. В итоге появление трещины изменило энергию пластины на величину

Изменение этой величины описывает средняя (результирующая) кривая на рис. 84. Как видно из графика, образование мелких трещин энергетически не выгодно. Но если в материале уже есть готовые трещины, то их дальнейший рост может стать выгодным.

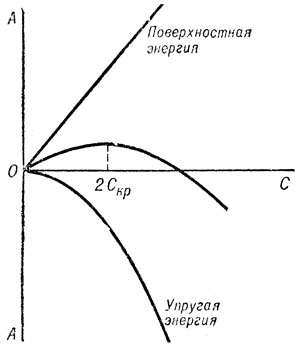
Рис. 146

Критический размер трещины 2 с_кр определяется из условия обращения в нуль первой производной dA/dc. В этой точке изменение энергии переваливает через максимум и дальше начинает уменьшаться:

Полученное Гриффитсом соотношение описывает критическую ситуацию. При заданном внешнем напряжении σ трещины длиной равной или меньше 2 с_кр = 2Eγ_s/σ² расти не будут. Трещины большей длины при этом же напряжении будут расти, причем из формулы Гриффитса следует, что при увеличении с можно уменьшать σ. Это фактически означает, что внешняя нагрузка уже не нужна: для завершения процесса разрушения достаточно той упругой энергии, которая была запасена в пластине к моменту достижения критической длины трещины.

К аналогичным соотношениям между приложенным напряжением и критической длиной трещины приводит анализ перенапряжений у ее вершины. Однако такой подход гораздо более сложен. Гриффитсу же удалось получить столь фундаментальный результат, вообще не рассматривая напряженного состояния материала у вершины трещины и не привлекая представлений о разрыве межатомных связей.

Теория Гриффитса объяснила катастрофический характер хрупкого разрушения, огромные ускорения при движении трещин, невозможность остановить процесс роста трещины, если он уже прошел критическую точку. Она дала положительный ответ на важнейший вопрос: "может ли работать материал с трещинами?". Она указала те предельные размеры трещин, с которыми еще может работать материал при заданном напряжении σ.

Рис. 85

Гриффитсовская формула позволяет решить и обратную задачу, которая чаще возникает в инженерной практике. Допустим, что технология получения или обработки какого-либо материала, который будет рекомендован конструктору, не гарантирует отсутствия трещин в изделии. Например, при сборке частей конструкции будет применяться сварка, которая часто вызывает образование трещин из-за резких перепадов температуры и по другим причинам (не случайно большая часть тех аварий, о которых мы рассказали, произошла со сварными конструкциями). В распоряжении технолога есть способы дефектоскопического контроля, которые позволят отбраковать детали с трещинами, не допустить их эксплуатацию в изделиях ответственного назначения. Но каждый метод дефектоскопии имеет некоторый порог чувствительности, поэтому можно с уверенностью утверждать лишь то, что в изделии не будет трещин длиннее определенного размера. Тогда это пороговое значение длины трещины и нужно будет подставить в формулу Гриффитса, чтобы найти напряжение σ_кр, при котором пропущенные дефектоскопом трещины еще не будут опасными. Конструктор обязан выбрать форму и размеры изделия так, чтобы при известной рабочей нагрузке напряжение в любом сечении было меньше найденного значения σ_кр.

Конечно, это лишь принцип расчета допустимого напряжения в конструкции. Здесь опущены многие вычислительные подробности, которые в реальном конструировании очень важны. Но несомненно, что сама возможность такого подхода базируется на теории Гриффитса.

Собственные эксперименты Гриффитса со стеклянными образцами (колбами), на которые он наносил острые надрезы, имитирующие трещины, дали великолепные результаты. Из теории вытекает, что произведение разрушающего напряжения σ_кр на √с_кр должно быть постоянным, поскольку γ_s и Е - это константы, характеризующие материал. Кроме того, поверхностное натяжение и модуль Юнга можно легко найти из независимых экспериментов и численно сопоставить величины σ_кр√с_кр и √Eγ_s. Совпадение и здесь оказалось хорошим.

Однако при переходе к металлам формула Гриффитса давала результаты, которые далеко не соответствовали реальности. Возникло сомнение в возможности использования этой теории применительно к металлическим материалам, хотя их поведение при хрупком разрушении качественно не отличалось от поведения стекла. Так же, как и стеклянные, металлические изделия в определенных условиях разрушались без заметной остаточной деформации при напряжении, не превышающем предела упругости. Так же разрушение становилось неуправляемым, "лавинным" процессом после достижения трещиной определенной длины. При понижении температуры многие металлы и сплавы, как и стекло, становились все более хрупкими. Трещины двигались в этих условиях примерно с такими же огромными скоростями и ускорениями.

Конечно, когда мы говорим о скорости и ускорении трещин, не следует забывать об условности этих понятий. Трещина ведь не является материальным телом, а речь идет о движении ее вершины.

Когда появилась возможность измерять очень высокие скорости движения трещин (например, методами скоростной киносъемки), были получены впечатляющие количественные результаты. Известный советский специалист в области разрушения В. М. Финкель приводит такие цифры. В хрупком металле трещина на докритической стадии процесса разрушения движется со скоростью порядка 1 мм/ч. После достижения критического размера за одну тысячную долю секунды скорость распространения трещины увеличивается до значений порядка 10000 км/ч! Следовательно, ускорение на этапе разгона - порядка 10⁸ м/с². Если бы пилотируемая космическая ракета развивала такое ускорение, космонавт испытывал бы десятимиллионную перегрузку! Даже беспилотным ракетам далеко до таких ускорений, а современным реактивным лайнерам далеко до таких скоростей. Что касается результатов столь оперативной работы трещин, то мы с ними уже знакомы по рис. 81 и 82. Отметим также, что подобные события значительно чаще случаются в холодное время года.

Итак, в чем же дело? Склонные к переходу в хрупкое состояние, как их называют, хладноломкие металлы разламываются как стекло, а классическая формула Гриффитса не работает. Испытания металлических образцов с трещинами показали, что в критический момент разрушения (момент, за которым следует быстрый рост трещины) напряжение в сотни раз больше, чем предсказывает гриффитсовская формула. Или наоборот, при данном разрушающем напряжении трещина должна была бы иметь такую длину, которая намного превышает размеры самого образца. И вместе с тем, сам этот критический момент существует, и все остальные следствия теории качественно выполняются.

Первым нашел причину этого несоответствия венгерский физик Орован, один из основоположников теории дислокаций. Он понял, что упругая энергия, которая высвобождается при росте трещины, расходуется не только на образование новых поверхностей, что при хрупком разрушении металла есть еще один потребитель энергии "змея", а сам "змей" должен быть, следовательно, более мощным, причем значительно. Этот потребитель энергии - пластическая деформация.

Действительно, стекло является аморфным материалом, и его способность давать остаточные деформации под действием напряжения определяется вязкостью. Вязкость аморфных тел резко увеличивается при понижении температуры. Например, снижение температуры всего на 20 градусов (от +80 до +60°С) увеличивает вязкость стекла в 10 000 раз. Значит, стекло всегда можно "заморозить" настолько, что его "течение" вообще станет невозможным. Уже комнатной температуры для этого достаточно. Стекло может реагировать на приложение внешней нагрузки либо изменением расстояний между атомами в пределах упругой деформации, либо (если в нем есть трещина, а напряжение достаточно велико, чтобы выполнялось условие Гриффитса) путем хрупкого разрушения. Металлы - тела кристаллические, и механизм их пластического течения иной. Пластическое течение, как мы знаем, связано с движением дислокаций. Сопротивление кристаллической решетки металлов движению дислокаций возрастает с понижением температуры, однако, далеко не столь резко, как вязкость аморфных тел. Вблизи абсолютного нуля предел упругости металла всего в несколько раз выше, чем при комнатной температуре.

Таким образом, раз около вершины трещины концентрируется огромное напряжение, некоторый объем металла всегда будет пластически деформирован. При распространении трещины по кристаллу в зону высоких напряжений у ее вершины будут попадать все новые источники дислокаций, которые трещина заставит работать, что приведет к увеличению плотности дислокаций. Короче говоря, когда трещина разорвет металл, поверхность излома будет пластически деформирована, и мы уже не сможем собрать и склеить осколки, восстановив исходную деталь с той же высокой точностью, как в случае стекла.

При хрупком разрушении металлов пластически деформированный слой, прилегающий к поверхности излома, существует всегда; речь может идти не о его наличии или отсутствии, а только о его толщине. В зависимости от условий работы металла (температуры, скорости приложения нагрузки, габаритов изделия, которые определяют полный запас упругой энергии, питающей процесс разрушения) его толщина может меняться от долей микрометра до многих десятков микрометров. Поскольку на пластическую деформацию затрачивается определенная работа, толщина слоя будет влиять на общие энергозатраты, связанные с разрушением. Чем быстрее бежит трещина, тем тоньше деформированный слой и тем в меньшей степени он деформирован, так как требуется некоторое время на приведение в действие дислокационных источников - они обладают определенной инерцией.

Все это не противоречит концепции Гриффитса, идее баланса энергий. Просто в его формуле к величине γ_s нужно добавить еще одно слагаемое γ_р - энергию, затрачиваемую на пластическую деформацию слоя материала, прилегающего к новой поверхности:

Теперь все становится на свои места, потому что слагаемое γ_р обычно на 2 - 3 порядка больше, чем γ_s, которую Орован назвал истинной поверхностной энергией, чтобы отличить ее от γ_р - эффективной поверхностной энергии. Первым слагаемым можно пренебречь ввиду его малости. И действительно, формулу Гриффитса - Орована часто записывают в виде

Важно, что величина γ_р не остается постоянной в течение всего процесса роста трещины. По мере разгона трещины, как уже было сказано, она уменьшается. Однако даже в самых неблагоприятных условиях она остается значительно выше γ_s. В. М. Финкель подсчитал, что эффективная поверхностная энергия стала бы равна истинной при скорости трещины 24 км/с. Трещина с такой скоростью двигаться не может; ее предельная теоретическая скорость составляет определенную долю (около половины) от скорости звука в металле, т. е. 2,5 - 3 км/с. Значит, на γ_р всегда приходится большая часть энергии "змея".

Однако, как ни "мал золотник" γ_s, а совсем пренебрегать собой он не позволяет. Его роль проявляется в том, что при хрупком разрушении монокристаллов поверхность излома всегда "придерживается" определенной кристаллографической плоскости в решетке. Эти плоскости называют "плоскостями скола". Например, кристаллы с ОЦК решеткой раскалываются по плоскости грани куба, и расчеты показали, что именно эта плоскость обладает наименьшей истинной поверхностной энергией. Таким образом, γ_s как бы "направляет" процесс хрупкого разрушения, ориентирует трещину в кристаллической решетке, а γ_р, хотя и берет на себя львиную долю энергии, но "действует" только в рамках уже заданной ориентировки трещины.

Значит, есть плоскости в кристалле, по которым он раскалывается сравнительно легко, если привести его в хрупкое состояние, например, охладив до низкой температуры. В предельном случае при хрупком разрушении кристалла в изломе обнажится определенная атомная плоскость - плоскость скола - и мы получим совершенно идеальное зеркало.

В металлах, даже самых хрупких, вид излома далек от этого идеала по уже известной нам причине - поверхность разрушения "испорчена" пластической деформацией. В сильный микроскоп мы увидим на ней ступеньки, впадины, бугорки и т. п. Рельеф поверхности излома может быть достаточно пологим, но это все же не идеальная атомная плоскость. Конечно, такой излом блестит, но зеркало это - "мутноватое". Излом, полученный в результате вязкого разрушения металла вообще не блестит; он матовый, хорошо рассеивает свет, так как поверхность его неизмеримо рельефнее, гораздо сильнее "испорчена" деформацией. Что касается стекла, то, как мы знаем, его легко "заморозить" и получить идеально хрупкое разрушение. Именно поэтому его так любил Гриффите. Но стекло - аморфный материал: оно не имеет кристаллической решетки, его атомы не образуют таких правильных построений, как атомы кристаллов. Следовательно, само понятие "атомная плоскость" здесь неприменимо. Поверхность хрупкого разрушения стекла, конечно, блестит, но далеко не так, как блестят бриллианты.

Вот мы и подошли ко второму вопросу, который поставили в начале этой главы. Почему сияет грань алмаза? Это, конечно, определяется его оптическими свойствами. Но здесь важно и еще одно обстоятельство. Алмаз - вещество кристаллическое, но гораздо более, хрупкое, чем самый хрупкий металл. Дело в том, что ковалентная связь, объединяющая атомы в решетке алмаза имеет строгую направленность, она далеко не так гибка, как в других веществах. Если мы вспомним механизм перемещения дислокаций в кристаллической решетке (рис. 42), то будет видно, что он требует значительных угловых смещений атомов относительно соседнего атомного слоя (хотя все это и происходит в малом объеме - вблизи края лишней полуплоскости). Ковалентная связь в алмазе не может выдержать таких деформаций, поэтому движение дислокаций в решетке алмаза практически исключено. Вот почему алмаз тверже всех металлов и всех существующих на Земле минералов, вот почему алмаз может резать все, что угодно, а его ничем разрезать или даже поцарапать нельзя.

Рис. 86

Однако, если нельзя разрезать, то можно расколоть, так как чем тверже материал, тем он обычно более хрупок. Задача ювелира - правильно найти плоскость скола и точно нанести удар. И тогда обнажившаяся грань алмаза будет сиять, как вечные снега Кавказа, поверхность которых, отшлифованная ветром времени, хорошо отражает солнечные лучи.

Новости и обзоры вилочных погрузчиков и складской техники вот тут.