§ 2. Как происходит сдвиг, или суровый боцман и хитроумный юнга

Очевидный геометрический результат скольжения одних частей кристалла по другим - появление ступенек на внешней его поверхности. При значительной пластической деформации ступеньки на поверхности становятся различимы с помощью обычного оптического микроскопа. Это было известно уже в начале XX века, и когда было установлено кристаллическое строение металлов, казалось, стал ясен и атомный механизм их пластической деформации. Действительно, как будто напрашивается вывод, что одна плотноупакованная атомная плоскость (и вся часть кристалла, ею ограниченная) сдвигается как жесткое целое относительно соседней атомной плоскости (и, значит, остальной части кристалла). Представления о том, что сдвиг одновременно охватывает всю площадь плоскости скольжения, не вызывали сомнений до 1924 г., когда известный советский физик Я. И. Френкель сделал оценку напряжения, необходимого для такого процесса.

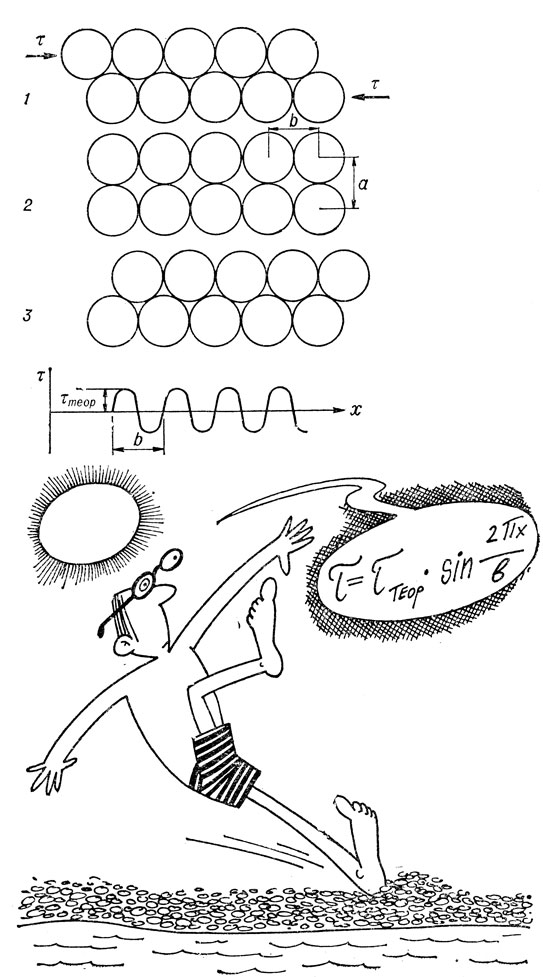
Рис. 39

Расчет Я. И. Френкеля был очень простым, а его результат - громоподобным. Если рассматривать сдвиг как одновременное смещение одной части кристалла по другой (рис. 39), то приложенное касательное напряжение т должно быть периодической функцией величины смещения атомов из исходного положения х.

Положения 1, 2 и 3 на рисунке - это положения равновесия, но в положении 2 потенциальная энергия системы атомов больше, чем в исходном положении 1. При переходе из 1 в 2 все атомы верхнего слоя должны как бы взобраться на горку, а при переходе в положение 3 атомы верхнего слоя как бы скатываются с горки. Эту аналогию, конечно, не следует понимать буквально, так как речь идет не о силах тяжести, а о силах межатомного взаимодействия.

Если продолжить сдвиг, то картина повторяется с периодом, равным межатомному расстоянию b в направлении скольжения. По сути дела положения 1 и 3 ничем не отличаются друг от друга в смысле взаимного расположения атомов, однако первый период нашей синусоиды соответствует появлению на правой и левой поверхностях кристалла ступенек высотой b, а каждый следующий - росту этих ступенек (всякий раз на величину b), т. е. увеличению сдвига.

Для оценочного расчета можно принять, что напряжение сдвига τ есть синусоидальная функция смещения х с периодом b и амплитудой τ_теор, которую и требуется найти:

Для малых смещений (при малых х величина sin х ≈ х)

С другой стороны, при малых смещениях справедлив закон Гука, который для случая сдвиговой деформации записывается в виде:

где G - модуль сдвига, γ - относительная величина сдвига, которая равна х/а. Приравнивая правые части двух последних равенств, получаем

а поскольку b ≈ а,

Конечно, это довольно грубая оценка, так как мы приняли, что смещения атомов значительно меньше межатомного расстояния и справедлив закон Гука. Поэтому не будем настаивать на коэффициенте 2π. Важно, что порядок величины τ_теор мы нашли правильно.

Неожиданно выяснилось, что касательное напряжение, необходимое для начала скольжения, - одного порядка с модулем сдвига! Причем здесь восклицательный знак? А притом, что к моменту появления расчета Я. И. Френкеля напряжения, при которых начинается пластическая деформация, и модули сдвига были определены экспериментально для многих металлов. Например, для чистого железа G ≈ 8·10⁴ МПа, а τ_упр ≈ 10 МПа. так что их соотношение отличается от расчетного в тысячу раз^*). Примерно такое же грубое расхождение с расчетом получилось и для других металлов.

^*

В чем же ошибка? Как оказалось, в самом исходном предположении об одновременном смещении всех атомов одной плоскости относительно соседней. Потребовалось, однако, 10 лет, чтобы прийти к такому очевидному сейчас представлению о том, что сдвиг не охватывает одновременно всю плоскость скольжения. Это кажется тем более странным, что подсказки мы теперь (задним умом!) находим на каждом шагу. Ведь если не удается сделать что-либо разом, "в лоб", то можно это же сделать постепенно.

Рис. 40

Представим себе, что на каком-либо судне боцман приказывает юнге передвинуть по палубе тяжелую якорную цепь (рис. 40). Юнга не имел бы никаких шансов на успех, если бы он пытался двигать цепь вправо, потянув за правый конец. Но, будучи хитроумным, он заходит с левого конца и сдвигает последнее звено цепи вправо настолько, насколько позволяет предпоследнее. Дальше он передвигает это предпоследнее звено, насколько позволяет третье от конца, и так же поступает с каждым следующим, пока не доберется до крайнего правого. В результате вся цепь перемещается вправо на длину одного звена, а поскольку в силах нашего юнги повторить эту операцию многократно, ему не страшен даже самый суровый боцман.

Тот же принцип использует в своем движении гусеница, так же опытный машинист, чтобы сдвинуть с места тяжелый состав, дает сначала задний ход, создавая зазоры в соединениях вагонов, а затем уже трогается вперед, как бы подключая к составу вагоны поочередно. И точно так же при скольжении в кристалле в положение 2 на рис. 39 переходят не одновременно все атомы верхнего слоя: они совершают это "восхождение" по очереди.

Постепенность распространения сдвига по плоскости скольжения обеспечивается особого рода дефектами кристаллической решетки, так называемыми дислокациями. Представление о дислокациях впервые появилось в 1934 г. в теоретических работах Поляни, Орована и Тейлора, опубликованных одновременно, но выполненных независимо друг от друга. Это представление позволило преодолеть вопиющее противоречие между реальным сопротивлением сдвигу и теоретическим. А с начала 50-х годов открывается подлинная "дислокационная эпоха" в металлофизике. Появляются мощные приборы - электронные микроскопы, позволяющие непосредственно убедиться в существовании дислокаций в металлах и изучать их поведение. Большая часть разработанных к тому времени теоретических положений, описывающих свойства дислокаций, блестяще подтвердилась на опыте.