§ 8. Как измерять скорость диффузии атомов, когда они не диффундируют?

Проблема диффузии - это одна из ключевых проблем физики твердого тела. Движущей силой диффузии обычно является различие концентраций растворенного вещества в разных объемах тела. Например, если в железе растворен углерод и в каких-то участках концентрация его атомов больше, чем в других, то атомы углерода будут двигаться в том направлении, где их меньше. Кристаллическая решетка большей части металлов соответствует одному из трех типов, показанных на рис. 26 упаковки ионов (шаров): гранецентрированная кубическая (рис. 26, а), гексагональная плотно-упакованная (рис. 26, б) и объемно центрированная кубическая (рис. 26, в).

При комнатной температуре железо существует в своей α-модификации и имеет решетку третьего типа. Атомы углерода располагаются в межузлиях решетки основного компонента, внедряются в промежутки между его атомами. Это, между прочим, не так легко, поскольку атомы металла плотно прилегают друг к другу. Например, в пору, соответствующую позиции в центре ребра куба, можно вписать шар радиуса 0,02 нм, так что даже маленький атом углерода не помещается в ней. Он с трудом "втискивается" на свое место и вызывает искажения в решетке, раздвигая соседние атомы железа.

В процессе диффузии атом углерода совершает "скачок" из того межузлия решетки железа, которое он занимает, в соседнее, такое же межузлие, затем в следующее и т. д. Каждый раз он с трудом "протискивается" между плотно прилегающими друг к другу атомами растворителя, прежде чем окажется в соседней позиции внедрения, где ему тоже тесно, но все же "терпимо". Для того чтобы диффундирующему атому совершить скачок, он должен обладать избыточной энергией (существует как бы некоторый энергетический барьер, который нужно преодолеть). Высота этого барьера и есть так называемая энергия активации диффузии Q. Чем выше температура, тем интенсивнее тепловые колебания атомов и тем легче преодолевается барьер.

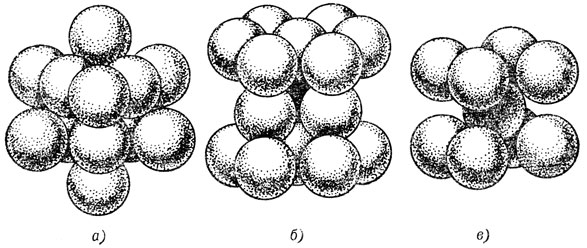
Рис. 26

Важнейшим показателем диффузионной подвижности атомов является коэффициент диффузии D. Согласно теории диффузии расстояние, на которое в среднем удаляется атом при диффузионных блужданиях за время t, пропорционально величине √Dt. Коэффициент диффузии имеет размерность см²/с, так что - размерность длины. Понятно, что коэффициент диффузии резко увеличивается с повышением температуры. Эту зависимость впервые установил шведский ученый С. Аррениус в 1889 г.:

Здесь k - постоянная Больцмана, a D₀ - коэффициент пропорциональности (предэкспоненциальный множитель)^*.

^*(В книге Б. С. Бокштейна "Атомы блуждают по кристаллу" (М.: Наука, 1983. Библиотечка "Квант", вып. 28) детально рассмотрена проблема диффузии в твердых телах и убедительно показана необходимость определения параметров диффузии.)

Чтобы измерить коэффициент диффузии какого-либо вещества в данном металле, его (или его радиоактивный изотоп) наносят на поверхность металла, затем нагревают и длительное время выдерживают образец при высокой температуре, чтобы получить достаточно толстый слой металла со сравнительно большой концентрацией диффундирующего вещества (хотя бы около 100 мкм - чтобы можно было хорошо видеть этот слой в микроскопе и точно измерить его).

Тогда, зная диффузионный путь √Dt и время отжига, этим методом можно измерить коэффициент D с достаточной точностью. А как быть, если нужно знать коэффициент диффузии при невысоких температурах, когда для получения такого слоя требуются месяцы? Здесь нет никакого преувеличения. Например, коэффициент диффузии углерода в железе при комнатной температуре порядка 10^-17 см²/с, и перемещение атома углерода всего на одно межатомное расстояние требует уже нескольких секунд. А при температуре 900 - 950°С насыщение поверхности железа углеродом на глубину 1 мм (это очень распространенный в технике процесс - цементация) происходит за несколько часов. Понятно, что все дело в величине коэффициента диффузии, который при 900 °С составляет примерно 10^-7 см²/с, т. е. на 10 порядков больше, чем при комнатной температуре (экспонента!). Скорость диффузии при этом увеличивается, соответственно, на 5 порядков.

Рис. 27

Между тем параметры диффузии при низких температурах знать очень нужно. В частности, в железе и стали уже при комнатной температуре идут важные структурные изменения, связанные с перемещениями атомов углерода на небольшие расстояния. Так как же быть? На помощь приходит уравнение Аррениуса. Поскольку D₀ и Q не зависят от температуры, достаточно измерить D при двух разных температурах (но обе должны быть высокими, так как нужен достаточно толстый слой). Тогда D₁ = D₀e^-Q/kT₁ и D₂ = D₀e^-Q/kT₂, и в этой системе двух уравнений остается два неизвестных. Найдя D₀ и Q, мы можем методом экстраполяции вычислить коэффициент диффузии при любой температуре.

Справедливость уравнения Аррениуса многократно проверена экспериментально, но ведь все эти эксперименты проведены в области достаточно высоких температур. Будет ли оно действовать и при низких температурах, правомерна ли экстраполяция? Есть основания сомневаться в этом, по крайней мере, в некоторых случаях. Например, в сильно деформированном металле при низких температурах есть множество дефектов кристаллической решетки (о них речь в следующей главе), которые могут сильно влиять на диффузионную подвижность атомов. А при высоких температурах, необходимых для диффузионного отжига, их число уменьшается в тысячи раз, и мы поневоле получаем искаженное представление об их роли в диффузионных процессах.

Так нельзя ли определить коэффициент диффузии непосредственно при низкой температуре, когда самой диффузии практически нет (точнее, когда она идет крайне медленно)? Здесь как раз и скажет свое веское слово метод измерения внутреннего трения.

Как мы уже установили, при растворении в решетке α-железа атомы углерода с трудом размещаются между атомами железа и вынуждены раздвигать их. Особенно сильно смещаются из нормальных положений два ближайших атома железа, расположенные по краям того ребра, центр которого занял атом углерода. Изобразим элементарную ячейку α-железа утрированно (рис. 28, а), увеличив расстояния между атомами. Если в данной ячейке находится атом углерода, то она искажается так, как (тоже утрированно) показано на позиции "в" - вместо куба мы получаем призму, у которой размеры по оси Z больше, а по двум другим осям - меньше, чем у исходного куба.

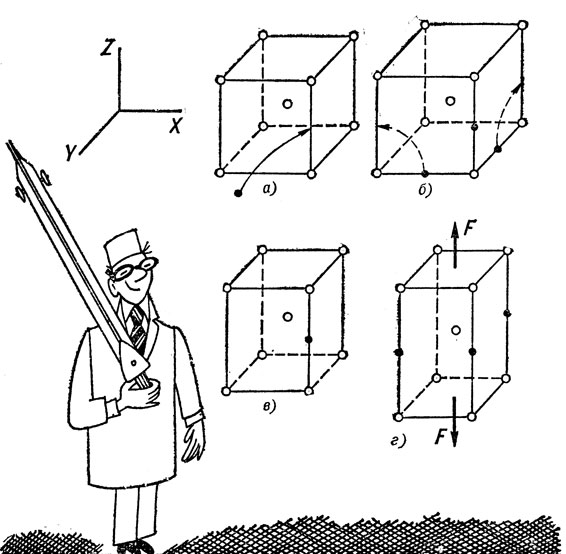
Рис. 28

Поскольку атомы углерода вызывают сильные искажения в решетке α-железа, в силу известного уже нам принципа Лe Шателье, оно не любит растворять углерод. При комнатной температуре предельная растворимость углерода в α-железе измеряется тысячными долями процента, так что один его атом приходится на несколько тысяч ячеек. Искажения быстро убывают по мере удаления от занятой атомом углерода ячейки, поэтому решетка в целом остается кубической. Кроме того, у атомов углерода нет никаких причин предпочитать ось Z другим осям, поэтому они в среднем равномерно распределяются по всем трем непараллельным ребрам куба. Условно эта ситуация изображена на позиции "б". Условность в том, что трем атомам углерода будет слишком тесно в одной ячейке. Если в одной из них атом углерода расположится в ребре, параллельном оси Z, то в другой удаленной на тысячи межатомных расстояний, он скорее всего окажется на ребре, параллельном оси X или Y и т. д.

Однако ситуация резко меняется, если мы приложим растягивающую силу, например, вдоль оси Z. Это само по себе вызывает искажения решетки того же вида, как на позиции "в". Вертикальные ребра растягиваются, остальные сжимаются (так же, естественно, изменяются внешние размеры самого растянутого образца). Теперь позиции внедрения, наиболее удобные для атомов углерода, перестают быть равноправными. Им удобнее располагаться в вертикальных ребрах, уже растянутых внешним напряжением, чем в горизонтальных - сжатых. Это вызовет перескоки атомов из позиций в осях X и Y в вертикальные ребра и вызовет их дополнительное растяжение. На рис. 28, г показано, к чему это приводит. Здесь та же условность, что и на позиции "б" - каждый атом совершает этот скачок, конечно, в пределах "своей" элементарной ячейки, но во всех ячейках, занятых атомами углерода, они будут стремиться перепрыгнуть в вертикальное ребро. Атом углерода ищет то место, где больше размер поры.

Но такие же скачки из одного ребра в другое атомы углерода совершают и при их диффузионном перемещении в решетке. Скорость скачка определяется диффузионной подвижностью атомов при данной температуре. Имеется простое соотношение между коэффициентом диффузии и временем скачка τ в решетке с длиной ребра а, которое было установлено А. Эйнштейном: D = а²/τ; это соотношение верно с точностью до коэффициента, зависящего от геометрии решетки и близкого к единице (переписанное в виде а = √Dτ, оно напомнит вам уже знакомое выражение - одно из основных уравнений диффузии).

Вот мы и получили типичный релаксационный процесс, вызывающий внутреннее трение. Будем циклически изменять нагрузку, приложенную вдоль оси Z (растяжение - сжатие). Если частота колебаний очень высока и время цикла мало по сравнению с τ, атомы не успеют совершить перескок, как напряжение уже изменит знак и ребра Z начнут сжиматься, становясь вместо более удобных, наоборот, более неудобными позициями внедрения. Атом углерода успевает лишь "захотеть" перескочить, как ситуация резко изменяется.

При слишком низких частотах все перескоки будут успевать следовать за изменяющимся напряжением. В ходе нагружения атомы успевают занять вертикальные ребра, в ходе разгрузки - перескочить обратно и создать первоначальное беспорядочное распределение по трем осям. Когда внешнее напряжение начнет сжимать кристалл вдоль оси Z, атомы из вертикальных осей будут переходить в горизонтальные и т. д., причем, поскольку время цикла велико по сравнению с τ, в каждый данный момент будет успевать устанавливаться именно то распределение атомов по трем осям, которое лучше всего соответствует величине и знаку напряжения.

Как мы уже знаем, в этих двух крайних случаях внутреннего трения нет. Оно достигнет максимума при частоте колебаний, отвечающей условию ωτ_р = 1, причем τ_р здесь близко по величине к τ - времени диффузионного скачка. Ведь не так уж важно, что именно является движущей силой скачков - различие в концентрации атомов углерода в разных местах, как при обычной диффузии, или периодически изменяющееся внешнее напряжение, как в нашем примере.

Теперь, измерив частоту ω, при которой внутреннее трение достигло максимума, и период решетки а, мы легко определим коэффициент D.

Интересно, что максимум внутреннего трения, обусловленный рассмотренным процессом, при комнатной температуре обнаруживается при частоте около 1 Гц, что очень удобно для измерений. Но вообще мы можем по своему усмотрению изменять и частоту колебаний, и температуру образца. Это дает возможность найти энергию активации того диффузионного процесса, который нас интересует. Например, при температуре Т₁, согласно уравнению Аррениуса, коэффициент диффузии равен D₁, а время скачка (по формуле Эйнштейна) τ₁. Если при этой температуре мы будем плавно изменять частоту колебаний ω, то внутреннее трение достигнет максимума при ω₁ = 1/τ₁. При температуре Т₂ максимум появится при другой частоте ω₂, так как коэффициент диффузии при этой температуре равен D₂ и время скачка τ₂. Так мы снова получаем два уравнения Аррениуса с двумя неизвестными D₀ и Q. Остальное - дело техники.

Вот мы и закончили самый, пожалуй, скучный раздел книги. Дальше, как мы рассчитываем, дело пойдет веселее. В "Записных книжках" написано: "Вы даже не представляете себе, каким я могу быть скучным и нудным". Если читатель улыбнется этой ильфовской шутке, то авторы могут себя поздравить. Если же скажет: "Вот именно", то они должны себе посочувствовать.