§ 8. Сверхпластичность

Разобравшись в дислокационном механизме пластической деформации металлов, мы должны теперь вернуться к самому понятию "пластичность". Будем считать пластичным материал, который выдерживает большую относительную деформацию без разрушения. При растяжении, например, мерой пластичности материала будет величина относительного удлинения к моменту разрушения, ε_разр. Обычные технические металлы и сплавы обладают значительной пластичностью. Весьма пластичными считают такие металлы, у которых ε_разр приближается к 50%. Это значит, что растягиваемый образец из такого металла может увеличить свою длину в 1,5 раза и лишь затем разрывается на 2 части.

Сверим приведенную цифру с нашим житейским опытом. Относительное удлинение наружных слоев материала при изгибе ε = В/2ρ, где В - толщина пластины или диаметр проволоки, а ρ - радиус дуги, в которую мы хотим превратить эту пластину или проволоку (этим соотношением мы уже пользовались в гл. 2). Простой расчет покажет, что пластину из материала, имеющего ε_разр = 50%, можно изогнуть до соприкосновения сторон (рис.49) и она при этом не сломается. Про такой материал каждый из нас скажет: "Да, он очень пластичен".

Рис. 49

Обратимся вновь к диаграмме деформации (рис. 13), вокруг которой развиваются главные события в нашей книге. Ясно, что пластичность материала - это протяженность линии диаграммы σ - ε по горизонтальной оси (за вычетом малой величины ε_упр, которой здесь можно пренебречь). На участке между σ_упр и σ_в пластическая деформация развивается равномерно по длине образца, все его диаметры при удлинении уменьшаются примерно в одинаковой степени. Способность материала к такой равномерной деформации связана с его наклепом.

Суть явления наклепа мы уже рассмотрели в § 6. Помните, "чем дальше в лес..."? По мере накопления пластической деформации е (или у) увеличивается плотность дислокаций ρ (ε∼ρ), и нужно все более высокое напряжение, чтобы испускаемые источниками дислокации могли "продираться через лес", который становится все более дремучим. Среднее расстояние между дислокациями равно 1/√ρ. Если принять, что напряжение, необходимое для движения дислокаций, обратно пропорционально среднему расстоянию между дислокациями - "густоте леса" (σ ∼ √ρ, то получится соотношение между напряжением и пластической деформацией (σ ∼ √ε), которое приближенно описывает ход диаграммы на интересующем нас участке.

Однако диаграмма характеризует поведение материала, так сказать, в макромасштабе. В микромасштабе картина несколько сложнее. В силу неоднородности процесса деформации ("работают" лишь определенные плоскости скольжения, а между ними остаются прослойки слабодеформированного материала), в силу природной неоднородности структуры самого материала и в силу действия других случайных обстоятельств диаметры образца в разных его участках могут несколько различаться. Допустим, что в ходе пластической деформации какой-либо участок длины образца уменьшил площадь своего сечения в большей степени, чем соседний. С давних пор такое местное утонение материала ученые ласково называют "шейкой", хотя на наш взгляд, здесь более уместным был бы столь же научный термин "талия".

Поскольку внешняя нагрузка одинакова для всех поперечных сечений образца, напряжение в шейке больше, чем в соседнем участке, и, казалось бы, здесь процесс пластической деформации должен развиваться быстрее, и именно здесь в конце концов произойдет разрыв образца. Но раз сечение в шейке уменьшилось сильнее, чем в соседней части, значит в этом месте материал испытал большую деформацию, плотность дислокаций возросла на большую величину, продолжение деформации требует больших напряжений. Участок с шейкой более "наклепан", чем соседний, который может деформироваться при меньшем внешнем напряжении. Поэтому процесс деформации в области шейки приостанавливается, а при дальнейшем растяжении площади сечения в разных участках выравниваются. Таким образом, наклеп обеспечивает устойчивость процесса "пластического течения" материала.

К сожалению, способность материала к наклепу, к упрочнению в ходе пластической деформации, как мы уже знаем, постепенно исчерпывается. На это указывает и сам вид зависимости σ ∼ √ε. Каждая новая "порция" деформации требует все меньшего прироста напряжения, угол наклона линии диаграммы к оси 8 становится все меньше и меньше. Это означает уменьшение пластичности материала - приближается момент его разрушения. Действительно, если теперь в каком-то участке образца появится шейка, то материалу уже нечем компенсировать рост напряжения, обусловленный уменьшением площади этого сечения. Процесс равномерного удлинения образца прекращается, и он деформируется теперь только в области шейки. Образец еще некоторое время удлиняется (линия диаграммы продолжается за точку В), но это удлинение происходит лишь за счет того, что диаметр шейки быстро уменьшается. Вскоре образец разделяется на 2 части.

Рис. 50

Итак, мы снова, кажется, в безвыходном положении. Устойчивость "течения" материала обусловлена его способностью к наклепу, но в кристаллических телах (металлах) плотность дислокаций вблизи точки В диаграммы деформации приближается к предельным значениям ρ = 10¹³ см^-2. Мы уже знаем, что при такой плотности дислокаций среднее расстояние между ними всего в 10 раз больше межатомного расстояния в решетке. Поскольку область сильных искажений кристаллической решетки около линии дислокации простирается на несколько межатомных расстояний, начинают перекрываться ядра соседних дислокаций. Здесь уже теряет смысл само понятие кристаллической решетки - все атомы довольно сильно смещены относительно своих нормальных положений: дислокации в таком "кристалле" размножаться и двигаться уже не могут. Правильный порядок во взаимном расположении атомов настолько нарушен, что наш "перенаклепанный" материал теперь больше похож на аморфное тело. С другой стороны, тесное сближение дислокаций способствует образованию разрывов, трещин (рис. 46), т. е. очагов разрушения.

Но минутку внимания! Слова "аморфное тело" наводят на некоторые размышления. Вспомним, как легко превратить в длинную тонкую нить кусочек смолы, какие тонкостенные сосуды можно выдувать из разогретого стекла. Аморфные вещества способны к огромным равномерным деформациям, процесс их течения очень устойчив, а никакого наклепа при этом нет. Почему же в этом случае появление первой же шейки не вызывает прекращение деформации в остальных участках растягиваемого образца и его быстрое разрушение?

При взаимном смещении слоев газа или жидкости возникает сила сопротивления, обусловленная вязкостью этих веществ и пропорциональная скорости смещения слоев. Сопротивление деформации аморфных твердых тел и обычных кристаллических металлов тоже зависит от скорости деформации. Эта зависимость описывается формулой:

Здесь σ - это внешнее напряжение, которое вызывает течение тела, К - константа, коэффициент пропорциональности, Δε - приращение относительной деформации за промежуток времени Δt, т. е. выражение в скобках - это скорость деформации. Показатель степени m называют показателем скоростной чувствительности. Он является мерой чувствительности сопротивления деформации к изменению скорости деформации.

Разница в поведении аморфных и кристаллических веществ при деформации связана с величиной показателя m. Обычно у металлов этот показатель гораздо меньше единицы, т. е. напряжение, вызывающее их течение, почти не зависит от скорости деформации. А вот у смолы или нагретого стекла он близок или равен единице.

Как же зависит характер процесса пластического течения материала от величины показателя m?

Отметим, что этот процесс в большинстве случаев развивается при постоянной скорости деформирования. Например, при растяжении образца в испытательной машине ее подвижный захват (рис. 12) обычно перемещается равномерно^*) с помощью электродвигателя. При появлении шейки напряжение в этом участке образца увеличивается, а остальные участки перестают деформироваться. Это значит, что обязанность увеличивать длину образца (в соответствии с неумолимо растущим расстоянием между захватами машины) берут на себя не все его участки, которые до этого дружно работали, а только небольшой, "брошенный в беде" участок в области шейки. Скорость деформации в этом объеме образца значительно возрастает, так как изменение расстояния между захватами Δl достигается за счет удлинения малого участка длины. Рост скорости деформации в соответствии с приведенной выше формулой ведет к увеличению напряжения, необходимого для продолжения течения. Чем выше показатель m, тем больше требуемый прирост а, и при достаточно высоких значениях m уже становится легче вовлечь в процесс течения другие участки с большей площадью сечения, чем продолжать деформировать тонкую, но "упрямую" шейку. Так шейка переходит на соседний участок длины образца, где ситуация повторяется и т. д. Получается, что шейка "бегает" вдоль оси образца, как бы выискивая слабые места. Но если показатель m имеет достаточную величину (опыт показал, что он должен быть не меньше 0,3), шейка нигде не может найти окончательного пристанища. Бегающая шейка "выглаживает" образец по всей его длине, процесс течения в макромасштабе остается равномерным.

^*(Вообще говоря, здесь требуется некоторое уточнение. При постоянной скорости движения захвата скорость деформации Δε/Δt в ходе растяжения постепенно уменьшается. Если разбить процесс накопления относительного удлинения ε = Δl/l₀ на ряд этапов, то одинаковый прирост длины Δl в каждом следующем этапе надо будет относить к все большей исходной (для данного этапа) длине l₀. В связи с этим либо приходится мириться с некоторым непостоянством скорости деформирования в обычных испытаниях на растяжение, либо применять специальные приемы для поддержания ее строго постоянной.)

Теперь дело за малым. Остается найти такие металлы или сплавы и такие условия их обработки, чтобы они обладали высокой скоростной чувствительностью сопротивления деформации, имели высокие значения m. Ведь в обычных условиях деформации металлов величина m имеет порядок 10^-2, и рассмотренный выше механизм не действует.

Как это часто случается, люди сначала сталкиваются с каким-либо явлением, затем разбираются в его причинах, а уже потом (в книжках) описывают все это в обратном хронологическом порядке. Не будем нарушать эту традицию.

Высокая пластичность

В 1934 г. преподаватель металлургии английского Армстронг-колледжа С. Пирсон опубликовал статью с отчетом о результатах испытаний образцов из сплавов свинца с оловом и висмута с оловом. Он обнаружил аномально высокую пластичность этих сплавов (рис. 51). Образцы при растяжении можно было удлинить в 20 раз! На это сообщение не последовало никакой реакции, и работа С. Пирсона вскоре была забыта.

Рис. 51

Второе рождение сверхпластичности относится к 1945 г., когда советские ученые А. А. Бочвар и З. А. Свидерская обнаружили необычное поведение сплавов цинка с алюминием. При небольшом подогреве эти сплавы становились чрезвычайно мягкими и давали огромные остаточные деформации. Академик А. А. Бочвар первым предложил сам термин "сверхпластичность", который в дальнейшем стал общепринятым, и указал на существенные черты явления. В частности, в его определении понятия сверхпластичности подчеркивается не только способность сплавов к большим деформациям, но и то, что сопротивление деформации сплава в этом состоянии очень мало. Твердость сплава цинка с алюминием была в несколько раз ниже твердости самого мягкого из компонентов.

В последующие годы исследования в области сверхпластичности получили бурное развитие. Были найдены многие десятки сплавов, которые можно деформировать на сотни и тысячи процентов (!) при ничтожно малых напряжениях порядка 1 - 10 МПа (!). Далее выяснилось, что сверхпластичность не является привилегией каких-то особых сплавов, а практически любой металл или сплав может быть переведен в сверхпластичное состояние. Для этого, конечно, необходимо соблюдение целого ряда условий.

Во-первых, металл или сплав должен иметь мелкие зерна - не более 10 мкм в поперечнике и чем мельче, тем лучше. Во-вторых, температура деформации должна быть достаточно высокой - обычно не ниже 0,5 Т_пл. В-третьих, скорость деформации должна находиться в определенных пределах - обычно 10^-6 ÷ 10^-3 процентов в секунду.

Рассмотрим смысл этих требований в связи с известными в настоящее время особенностями механизма сверхпластической деформации металлов. В этом процессе важная роль, несомненно, принадлежит так называемому зернограничному скольжению. При сверхпластическом течении, в отличие от обычной пластической деформации (рис. 38), зерна не вытягиваются в направлении действия напряжения, а остаются круглыми. Но при этом они могут менять своих соседей, так что в конечном счете число зерен (а не их размер) в поперечном сечении образца уменьшается, а в направлении оси - увеличивается. Они как бы перекатываются друг по другу наподобие песчинок или гальки, хотя ситуация в металле, конечно, гораздо сложнее. Ясно, однако, что чем более развита межзеренная поверхность, т. е. чем мельче зерна, тем легче реализуется этот своеобразный механизм деформации.

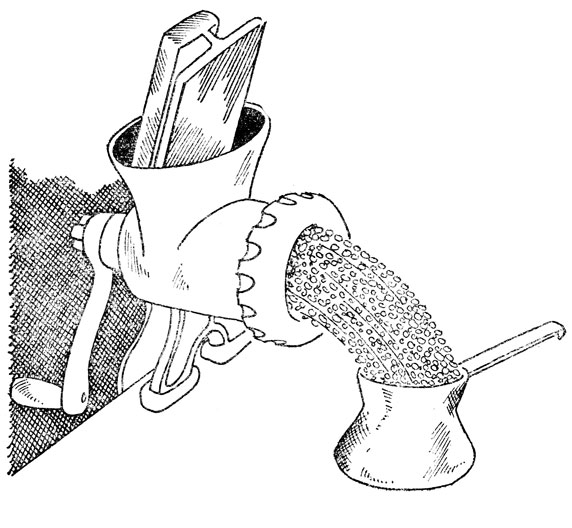
Рис. 52

У каждого зерна в поликристалле более десятка соседей, а форма зерен далека от правильной шарообразной, хотя мы и назвали их круглыми. Шарами, как мы помним, даже при самой плотной их упаковке можно занять лишь 74% объема. Зерна на самом деле имеют форму многогранников и при их взаимных перемещениях и поворотах около границ должны образовываться зазоры. Эти поры являются очагами разрушения, из них вырастают трещины, которые могут разорвать образец. Но этого не происходит, и процесс течения спокойно развивается. Значит, одновременно с зернограничным скольжением должны срабатывать и какие-либо механизмы "залечивания" очагов разрушения, что впервые было отмечено А. А. Бочваром еще в 1945 г. Залечивание, или "взаимное приспособление", зерен может быть обеспечено и обычной дислокационной деформацией, и так называемым диффузионным массопереносом. Последние два процесса выполняют не только вспомогательные функции (залечивание пустот), но могут служить и самостоятельными механизмами деформации металла в состоянии сверхпластичности.

О том, как движение дислокаций приводит к деформации кристалла, мы уже говорили. Поэтому здесь обсудим в общих чертах только диффузионный массоперенос. В этом процессе участвуют вакансии - незанятые узлы решетки. В соответствии с принципом Ле Шателье в растянутых участках решетки вакансии образуются легче, чем в неискаженной решетке. Дело в том, что появление вакансии приводит к сближению атомов, окружающих незанятый узел, т. е. как бы снимает локальное напряжение в растянутой решетке. Таким образом металл сопротивляется внешнему воздействию. В сжатых областях образование вакантных мест, наоборот, невыгодно. Таким образом, в областях растяжения концентрация вакансий будет выше нормы, а в сжатых участках - ниже. Возникающий вследствие этого поток вакансий, направленный на выравнивание их концентрации, соответствует встречному потоку атомов: в местах, откуда уходят вакансии, увеличивается число атомов и наоборот (стрелками показано направление движения атомов от сжатых участков к растянутым - рис. 53). Как видно, этот механизм сам по себе работает в нужном нам направлении. Он же может обеспечивать (самостоятельно или вместе с дислокационным скольжением) ликвидацию зазоров у границ (рис. 54). На этом же рисунке видно, как зерна меняют своих соседей - зерна 1 и 3 вошли в соприкосновение, а зерна 2 и 4, наоборот, теперь не имеют общей границы. Видно также, что число зерен в направлении растяжения в результате такого процесса будет увеличиваться, а в поперечных направлениях - уменьшаться. Поскольку и скольжение дислокаций и образование вакансий облегчаются с ростом температуры, становится понятным смысл второго условия (T_деф ≥ 0,5T_пл). Мы уже знаем, что понятие низкой или высокой температуры для данного металла обычно имеют смысл в сопоставлении с его температурой плавления. Именно поэтому легкоплавкие сплавы С. Пирсона проявляли сверхпластичность при комнатной температуре, которая была для них достаточно высокой, А. А. Бочвару потребовалось подогревать свои сплавы до 150 - 200°С, а для перевода в сверхпластичное состояние, скажем, титановых сплавов, нужны температуры около 1000°С.

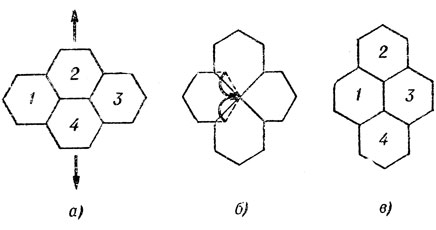
Рис. 54

Что касается третьего условия проявления сверхпластичности, то нам поможет самый общий, по существу даже формальный, подход к явление. Если деформация развивается с постоянной скоростью при низком и практически постоянном напряжении, то мы можем представить себе это как результат равновесия процессов упрочнения и разупрочнения материала. Упрочнение увеличивает напряжение, необходимое для продолжения течения, а разупрочнение снижает его, и в итоге оно остается постоянным. Упрочнение связано с необходимостью обеспечить взаимные повороты и перемещение зерен, действие дислокационных источников, образование вакансий и т. д. Разупрочнение - с исчезновением дислокаций на границах зерен, с движением диффузионных потоков, выравнивающих концентрацию вакансий и тем самым снимающих перенапряжение в различных объемах материала. Для реализации всех этих процессов требуется определенное время (кстати, тем меньшее, чем меньше расстояния между границами зерен).

При очень малых скоростях деформации для протекания разупрочняющих процессов времени всегда достаточно, а при слишком высоких - наоборот, всегда не хватает. Равновесие возможно в некотором промежуточном интервале скоростей деформации, но его довольно легко нарушить. Стоит увеличить скорости, как упрочнение начинает преобладать над разупрочнением, и требуемое для дальнейшей деформации напряжение резко возрастает. Именно в этом интервале скоростей материал обнаруживает высокую скоростную чувствительность течения. Значение m становится выше 0,3 (иногда m достигает 0,8 - 0,85), что и является признаком перевода материала в сверхпластичное состояние.

Рис. 55

Таким образом, выяснилось, что показатель скоростной чувствительности сам зависит от скорости деформации и достигает максимума в указанном выше интервале скоростей.

Рис. 56

К сожалению, все три условия сверхпластичности затрудняют практическое использование этого замечательного явления. Не всегда легко получить достаточно мелкозернистую структуру материала. Для поддержания заданной температуры процесса требуется подогреваемый деформирующий инструмент, так как в силу третьего условия сам процесс занимает значительное время. Даже самая высокая скорость деформации, при которой еще реализуется сверхпластичность (10^-3 процентов в секунду), гораздо ниже обычных скоростей, используемых в практике деформации металлов. Однако и вопросы производительности, и другие технические вопросы, связанные с использованием сверхпластичности, в принципе разрешимы, а преимущества здесь очевидны: из металла за одну операцию можно "выдувать" такие же ажурные изделия, как из стекла или пластмасс иллюстрирует возможности металла в сверхпластичном состоянии. Лист из "бочваровского" сплава толщиной 0,03 мм под действием давления газа выдувается в полную сферу диаметром чуть более 100 мм. Не правда ли - неплохой "мыльный пузырь". На рис. 56 показана деталь оборудования кабины самолета "Конкорд", изготовленная за один прием из того же сплава. Ранее такие детали делали из пластмасс, но требования противопожарной безопасности заставили инженеров вновь обратиться к металлу, который оказывается способен и на такое.

Рис. 57

А это изделие (рис. 57) получено в Московском институте стали и сплавов. Снимок, вероятно, в комментариях не нуждается.

Способность металлов в сверхпластичном состоянии деформироваться без разрушения, по-видимому, не ограничена. После того как в лабораториях были получены относительные удлинения до 5000% (50-кратное увеличение длины), погоня за рекордами прекратилась. Ограничения здесь носят уже чисто технический характер - не хватает длины печей (если сплав необходимо нагревать), не хватает расстояния между стенами комнаты или потолком и полом. А металл мог бы течь и дальше!