§ 4. Сколько требуется дислокаций?

Мы не будем рассматривать здесь другую категорию линейных дефектов - так называемые винтовые дислокации, хотя они играют не менее важную роль в процессах пластической деформации, чем краевые. Строение винтовых дислокаций и их движение в решетке имеют свои отличительные особенности, но пусть они останутся за кадром. Будем считать, что мы в основном выяснили, как происходит скольжение в кристаллах.

Но вслед за фундаментальными вопросами "что, как и почему?" обычно следует уже более прозаическое: "сколько?". Ответ на этот простой вопрос иногда ставит новые "как и почему", в чем мы уже могли убедиться. Например, Френкель первый задался вопросом, какое напряжение (сколько мегапаскалей) нужно приложить, чтобы вызвать сдвиг. Результатом было появление теории дислокаций, которая сыграла революционную роль во многих разделах физики твердого тела.

Итак, сколько дислокаций нужно, чтобы обеспечить сдвиговую деформацию заданной величины? Это один из первых вопросов, на который должна была ответить количественная дислокационная теория. Предположим, что касательное напряжение т стремится вызвать сдвиг у вправо части кристалла с размерами l₁ и l₂ (рис. 43), причем в процессе участвует n дислокаций, скользящих в параллельных плоскостях. Введем количественную меру - плотность дислокаций ρ, которая определяется как число дислокаций на единицу площади поверхности кристалла: ρ = n/l₁l₂. Иногда используется другая мера плотности дислокаций - суммарная длина всех дислокационных линий в единице объема. Если предположить, что все дислокации прямолинейны и перпендикулярны площадке, на которой мы фиксируем их выходы на поверхность, то эти меры идентичны. Вообще же они не совпадают, но при оценках можно пользоваться любой из них. Для простоты мы выберем первую.

Когда дислокации пробегут путь l₁ от левой до правой грани кристалла, каждая из них даст на поверхности ступеньку величиной b (см. рис. 42).

Пока ступеньки есть только на левой грани кристалла, значит изменение его размера в направлении оси х, связанное с одной дислокацией, на этой стадии деформации меньше b. Это изменение размера δ, составляет такую же долю от b, какую пробег дислокации я составляет от l₁:

Понятно, что при х = l₁ получим δ = b.

Полное изменение Δ, размера кристалла в направлении оси х будет равно сумме тех смещений δ, которые связаны с каждой дислокацией:

где n - число дислокаций, а х - усредненная по всему кристаллу длина пробега дислокаций.

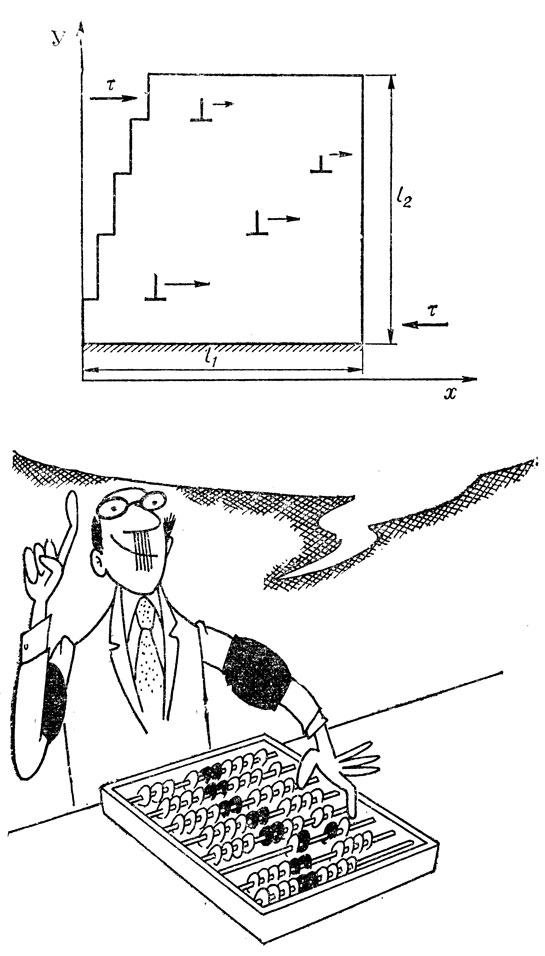
Рис. 43

Относительная деформация сдвига в плоскости ху равна изменению размера вдоль оси х, деленному на исходный размер вдоль оси у:

Но n/l₁l₂ - это и есть плотность дислокаций ρ, поэтому

Теперь можно сделать интересующую нас оценку. Примем, что средний пробег дислокаций равен среднему расстоянию между ними, которое в свою очередь, очевидно, равно 1/√ρ. Тогда γ = b√ρ. Так как b в металлических кристаллах равно (2÷3)·10^-8 см, для получения деформаций порядка десятка процентов нужно ∼ 10¹³ дислокаций на 1 см².

Рис. 44

Такая плотность дислокаций близка к предельной, так как среднее расстояние между ними при этом - порядка десятка межатомных расстояний. Еще немного - и начнут уже перекрываться искаженные области решетки вблизи оси дислокаций и не останется атомов, занимающих нормальные позиции в ее узлах. И тем не менее в сильно деформированных металлах экспериментально измеренная плотность дислокаций действительно приближается к этой цифре. Сама же цифра должна производить весьма серьезное впечатление, так как она гласит, что в кусочке сильно деформированного металла размером с булавочную головку суммарная длина дислокационных линий превышает расстояние от Земли до Луны!